This is not the end.

0%

图论练习题

Posted on Edited on

LOJ2146 「SHOI2017」寿司餐厅

把$mx^2 + cx$拆一下就是：只要吃的寿司里面有代号为$x$的就要付出$mx^2$的代价；每吃一种代号为$x$的寿司就要付出$x$的代价。直接令$d_{i,i}$减掉$a_i$，就可以不再考虑$cx$这部分。

对每个区间$[l,r]$建一个点，权值为$d_{l,r}$；对每个代号建一个点，权值为$-mx^2$。如果选了$d_{l,r}$就必须选$d_{l,r-1}$和$d_{l+1,r}$，如果选了$d_{i,i}$就必须选$ma_i^2$。求出这张图的最大权闭合子图即可。

Code

LOJ2100 「TJOI2015」线性代数

把$A$想象成$\{1,2,\cdots n\}$的一个子集，$0$表示不选，$1$表示选。则：

对每个$B_{i,j}$和$C_i$建一个点，权值分别为$B_{i,j},-C_i$，要求如果选了$B_{i,j}$则必须选$-C_i$和$-C_j$。求出这张图的最大权闭合子图即可。

Code

UOJ41 【清华集训2014】矩阵变换

考虑什么样的方案是不合法的：第$x$行选择了$y$，并且存在另一行$x’$，$y$在$x’$行的出现的列编号大于$y$在$x$行出现的列编号，且$x’$行选择的那个数字的列编号在$y$之后。

可以转化成稳定婚姻问题：由于要求每列中每个数至多出现一次，所以每一行选择的数显然是不同的，所以可以把问题看作求行和数字的匹配。对于每一行，在那一行出现的列编号越小的数字越好；对于每一个数字，它在其中出现的位置越靠后的行越好。这样求出的解显然能够规避上面说的不合法情况。

Code

LOJ2052 「HNOI2016」矿区

分母很容易算，考虑怎么求分子。

将平面图转化成对偶图之后，以无穷域为根，求出一棵dfs树，并处理出子树内的块的矿量和。

考虑给出的开发区域的每一条边：如果它在对偶图中是非树边则不管它；如果它是树边，且它连接的两个点中，开发区域外的点是父亲，那么就让总和加上区域内的那个子树的权值；如果它是树边，且它连接的两个点中，区域里的点是父亲，那么就让总和减去区域外的那个子树的权值。

注意对偶图中可能是有重边的。

Code

TopCoder14750 HeroicSchedule

可以在vjudge上提交

下面用$n$表示点数，$m$表示边数。

由费用流的过程可以知道，将所有的任务按照收益从大到小排序之后，依次考虑每个任务，能够加入则加入，则一定能够得到最优的解。

尝试加入的过程就是求匹配的过程，考虑用匈牙利算法来实现这一部分。直接做的复杂度是$O(n^2m^2)$的。

发现尽管边数很大，但是遍历边集的时候我们实际上是在一个区间内的点中找到一个vis不为$0$的点，用set就可以在$O(\log m)$的时间内完成。复杂度优化到$O(n(\log m + m\log m))$。

更进一步观察发现，只要当前已经求出的匹配没有变化，就没有清空vis的必要。而匹配的大小只会从$1$变到至多$m$，也意味着匹配至多会改变$m$次。所以我们的等到匹配改变的时候才清空vis，就能把复杂度做到$O(n\log m + m^2 \log m)$。

Code

HDU6431 NewNippori

分别求出$maxflow(x,y)$为1,2的点对的数量，就可以算出答案。

$maxflow(x,y)=1$的点对即不在同一个边双连通分量的点对。

$maxflow(x,y)=2$的点对一定在同一个边双连通分量且可以通过割掉两条边使它们不连通。

对每个边双连通分量分别考虑。首先求出一棵dfs树。考虑割掉哪些边能够把这个边双分成不连通的两个部分：

  • 割一条树边和一条非树边。我们称一条非树边覆盖了一条树边，当且仅当非树边的两个端点在树上的最短路包含了那条树边。由于这是一个边双，所以每条树边至少被一条非树边覆盖；又由于我们只能割一条非树边，而覆盖了我们割的那条树边的非树边必须全部被割掉，所以我们割的树边一定恰好只有一条非树边覆盖了它。把那条树边和覆盖它的非树边割掉，可以把dfs树上树边两侧的部分割开。

  • 割两条树边。考虑这两条树边割开之后树边将dfs树分成了三部分：
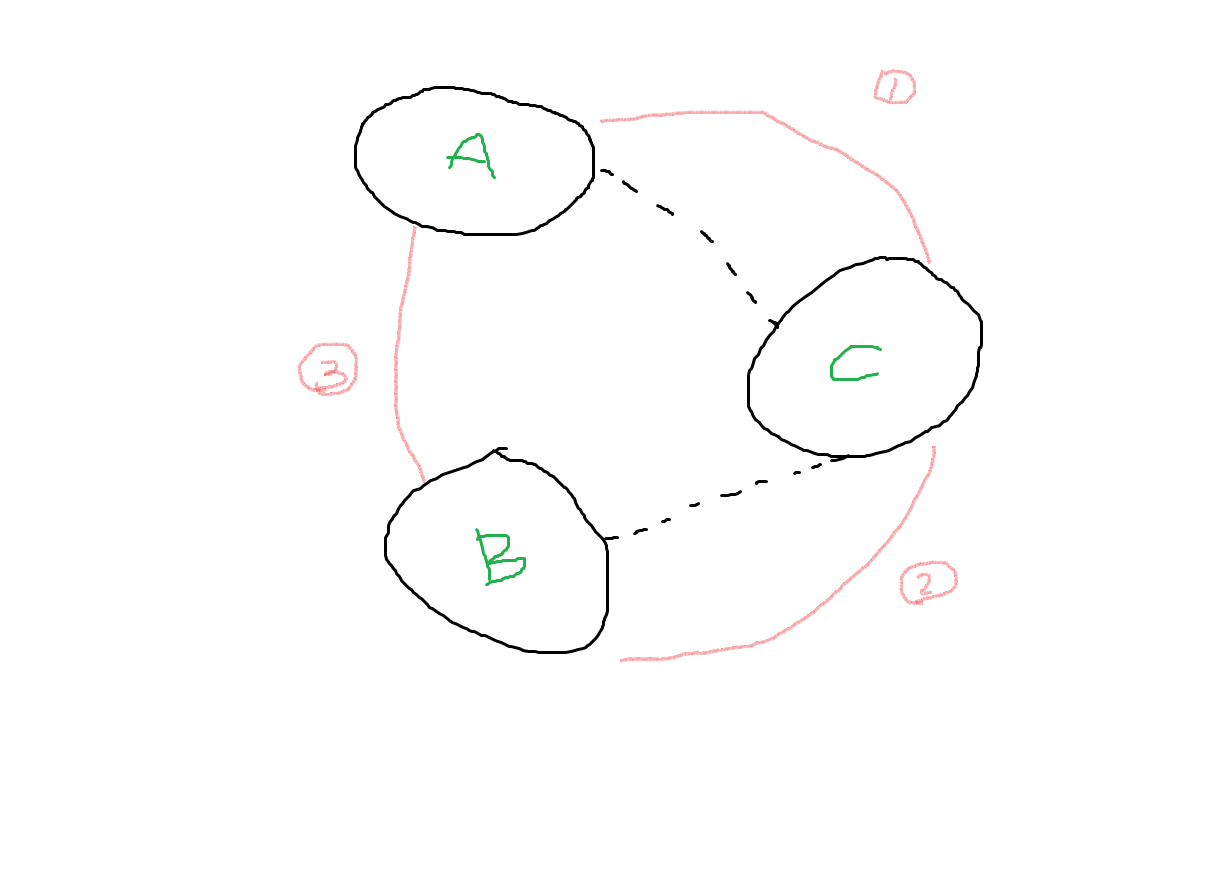
    hdu6431.png
    其中黑色的圈表示树上的连通块，黑色的虚线表示割掉的树边，1，2，3分别表示在这三个连通块之间的非树边。

    • 如果1存在，由于每条树边都至少有一条非树边覆盖了它，所以2和3至少有一条边存在，所以这时三个块仍然连通。2存在同理。
    • 如果这三种边中，只有3这种边存在，发现割了两条树边之后，A和B组成的连通块和C之间没有边。

    所以，割的两条树边一定满足：所有的非树边要么同时覆盖这两条边，要么同时不覆盖这两条边。

如何判断覆盖了两条树边的非树边集合是否相同：可以用与uoj207那道题一样的方法，给每一条非树边随机一个$[0,2^{64})$的权值，设每个点的权值为所有以它作为一端的非树边的权值的异或和。则当两个点的子树内所有点的权值的异或和相同的时候，我们认为这两个点到它们的父亲的那两条边被非树边覆盖的情况相同；当某个点子树内点的权值异或和为某条非树边的权值，我们就认为这个点到父亲的那条边只被那条非树边覆盖。

首先统计跨越了只被一条非树边覆盖了的树边的点对的贡献，然后把这些树边都断开。下面考虑的是断开了这些边之后的每个连通块。

对每个点$x$，统计出满足下面条件的点的数量：存在一对树边，割开之后能够把$x$和这个点隔开，且$x$位于与两条树边都相邻的那个连通块里面（上图中的连通块C）。

由于我们求的是dfs树，所有的非树边都是返祖边，不存在横叉边。所以，被覆盖情况相同的两条树边也一定是祖孙关系。

考虑把$x$夹在了中间的那些可以割掉的树边对：

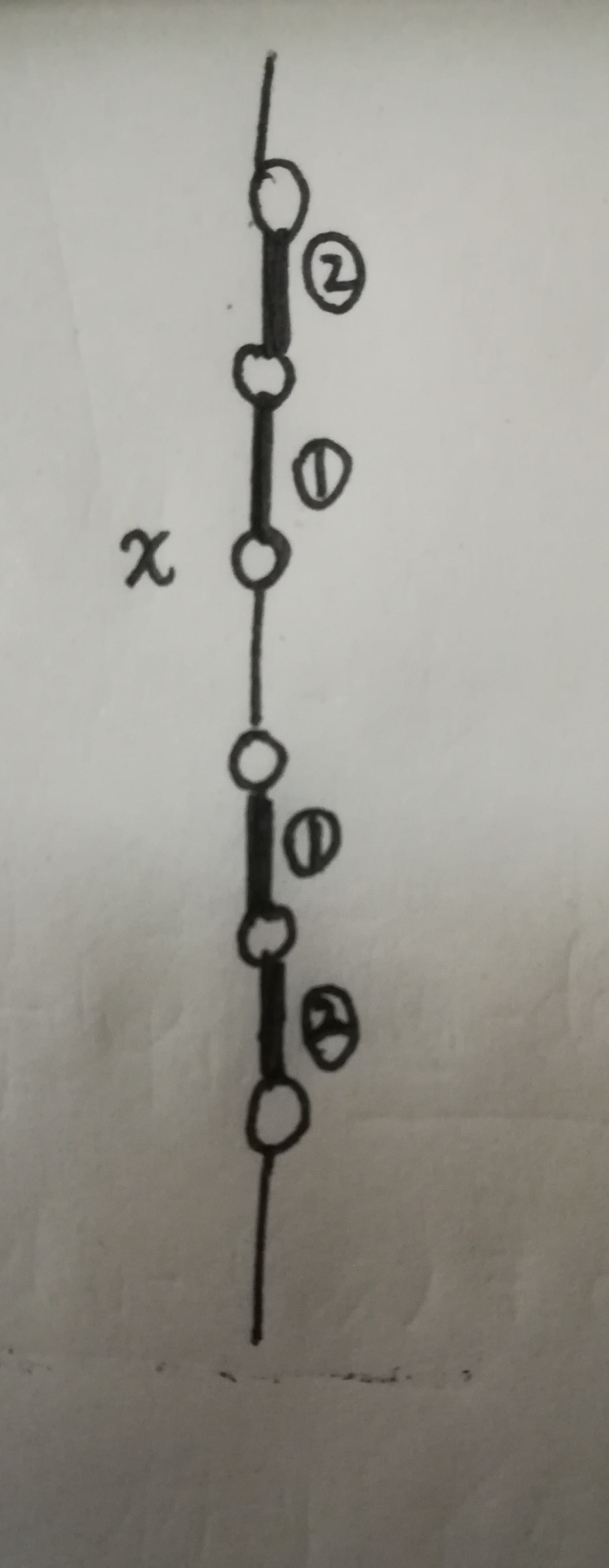
观察到：

  • 对于某条树边，能够和它配对的边显然都在一条祖孙链上。
  • 不可能存在两对树边$(u,v),(x,y)$，满足$dep_u < dep_x < dep_v < dep_y$。

所以，对于某个$x$，把它夹在了中间的树边对一定满足：假设这些树边对按照在$x$的上面的那条边的深度升序排序得到的序列是$w_1,w_2,\cdots w_k$，那么按照在$x$的下面的那条边的深度升序排序得到的序列就是$w_k,w_{k-1},\cdots w_1$。我们只需要找出$w_k$：$w_k$把整棵树分成三部分中不包含$x$的那两部分的大小，就是能够通过割两条树边与$x$隔开的点数。

对连通块进行dfs，到达某个点$u$的时候，先递归处理$u$的子树内的点，然后再处理$u$到它的父亲之间的这条边与$u$的子树内的边配对所能够产生的贡献。

找出最后一次访问到的与$e(u,fa_u)$的覆盖情况相同的边$e’$，如果这条边不在$u$的子树内说明$e(u,fa_u)$无法与子树内的边配对；否则，我们只需要考虑$e(u,fa_u)$与$e’$配对就可以了（因为对每个$x$我们只关心包含了它且离它最近的边对，$e(u,fa_u)$和其它的边配对显然不满足这个条件）。我们找出$e’,e(u,fa_u)$之间还没有找到最近的树边对的点，统计它们的贡献，并把它们标记为已经找到了最近的树边对的点。实现上可以用一个数组$ex[u]$来记录每个点的子树内还没有找到最近树边对的点数；由于$e(u,fa_u)$已经和$e’$配对了，所以$e(u,fa_u)$上方的边不可能与$e(u,fa_u)$和$e’$之间的边配对，因此我们不需要维护$e(u,fa_u),e’$之间的点的$ex$，只对$ex[u]$做出相应的更新就可以了。

总复杂度$O(n+m)$或者$O(n\log n + m)$（取决于使用map还是hash_table）

下面是我的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#define PB push_back
#define MP make_pair
#define PII pair<int,int>
#define FIR first
#define SEC second
#define ll long long
#define ull unsigned long long
using namespace std;
template <class T>
inline void rd(T &x) {
	x=0; char c=getchar(); int f=1;
	while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
namespace RNG {
    ull seed=13244074693642402ull;
    ull rnd() {
        seed^=seed<<13,seed^=seed>>7,seed^=seed<<17;
        return seed;
    }
}
using RNG::rnd;
const int N=1e5+10,M=3e5+10;
struct ed { int to,id; };
vector<ed> G[N];
ll ans0,ans1;
int n,m;
namespace tree {
    int In[N],vis[N];
    vector<int> son[N];
    set<ull> val;
    ull xi[N];
    int vise[M];
    void dfs1(int u) {
        vis[u]=1;
        for(int i=0;i<G[u].size();++i) if(!vise[G[u][i].id]&&In[G[u][i].to]) {
            int v=G[u][i].to; vise[G[u][i].id]=1;
            if(vis[v]) {
                ull tmp=rnd();
                val.insert(tmp),xi[u]^=tmp,xi[v]^=tmp;
            }
            else son[u].PB(v),dfs1(v);
        }
    }
    map<ull,int> mp;
    int _size,__size;
    int ex[N];
    void dfs3(int u) {
        ex[u]=1;
        int pre_c=mp.count(xi[u])?mp[xi[u]]:0;
        for(int i=0;i<son[u].size();++i)
            if(vis[son[u][i]]!=2) dfs3(son[u][i]),ex[u]+=ex[son[u][i]];
        int c=mp.count(xi[u])?mp[xi[u]]:0;
        if(c&&c!=pre_c) {
            ans1+=2ll*(ex[u]-ex[c])*(ll)(_size-(ex[u]-ex[c]));
            _size-=ex[u]-ex[c];
            ex[u]=ex[c];
        }
        mp[xi[u]]=u;
    }
    int dfs2(int u) {
        int tot=1;
        for(int i=0;i<son[u].size();++i)
            tot+=dfs2(son[u][i]),xi[u]^=xi[son[u][i]];
        if(val.count(xi[u])) {
            ans1+=tot*(ll)(__size-tot);
            mp.clear(),_size=tot,dfs3(u);
            vis[u]=2,tot=0;
        }
        return tot;
    }
    void sol(vector<int> &a) {
        __size=a.size();
        for(int i=0;i<a.size();++i) In[a[i]]=1;
        dfs1(a[0]); val.insert(0);
        dfs2(a[0]);
        val.clear();
        for(int i=0;i<a.size();++i) In[a[i]]=0;
    }
    void init() {
        for(int i=1;i<=n;++i) xi[i]=vis[i]=0,son[i].clear();
        for(int i=1;i<=m;++i) vise[i]=0;
    }
}
int st[N],top;
int dfn[N],low[N],id;
vector<int> a;
void tarjan(int u,int lasteid) {
    dfn[u]=low[u]=++id,st[++top]=u;
    for(int i=0;i<G[u].size();++i) if(G[u][i].id!=lasteid) {
        int v=G[u][i].to;
        if(dfn[v]) low[u]=min(low[u],dfn[v]);
        else tarjan(v,G[u][i].id),low[u]=min(low[u],low[v]);
    }
    if(low[u]==dfn[u]) {
        do a.PB(st[top]); while(st[top--]!=u);
        tree::sol(a),ans0+=a.size()*(n-a.size());
        a.clear();
    }
}
int main() {
    int T; rd(T);
    while(T--) {
        rd(n),rd(m);
        for(int i=1,x,y;i<=m;++i) {
            rd(x),rd(y);
            G[x].PB((ed){y,i}),G[y].PB((ed){x,i});
        }
        tarjan(1,0);
        ans0/=2,ans1/=2;
        ll ans2=n*(ll)(n-1)/2-ans0-ans1;
        printf("%lld\n",ans0+ans1*2+ans2*3);
        for(int i=1;i<=n;++i) G[i].clear(),dfn[i]=0; id=top=0;
        ans0=ans1=0;
        tree::init();
    }
    return 0;
}