TopCoder14929 MaxSquare
设$s_i$表示$B$的前缀和。
显然最优的时候$r_2=r_1,l_2=l_1$,所以
想象成平面上有$n$个点$(i,s_i)$,那么上式等价于:选择两个点作为矩形的两个相对的顶点,矩形的面积的最大值。
我们先考虑一个点作为左下角的点,另一个点作为右上角的点的情况(一个点作为左上角,另一个作为右下角是同理的)。
显然对于作为左下角的那些点来说,如果$i < j\wedge s_i < s_j$,那么$(i,s_i)$是没有用的。右上角同理。
所以有用的点会形成这样的分布:

然后对于每个右上角的点,考虑矩形面积在左下角的哪一个点取到最大值。观察下图:
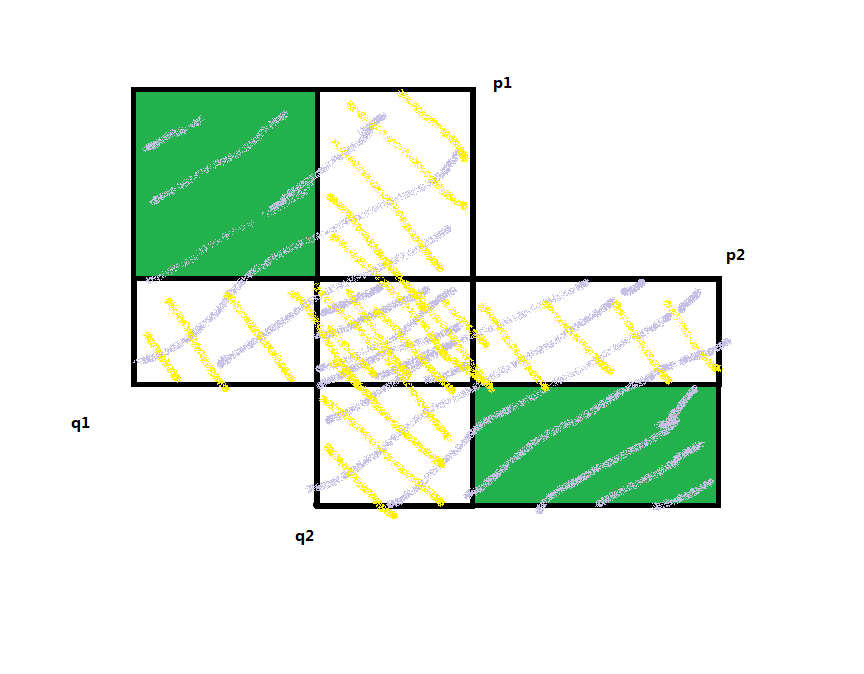
可以得到结论:如果对于$p_1$,$q_2$比$q_1$优,那么对于$p_2$,$q_2$一定比$q_1$优秀。
证明:考虑反证
也就是上图中绿色标出的部分,其面积要小于$0$,推出了矛盾。
用经典的决策单调性的分治算法,就可以在$O(n\log n)$的时间内解决问题。
CF908H New Year and Boolean Bridges
$f(i,j) \operatorname{AND} f(j,i) =1$的肯定在同一个SCC里面,而$f(i,j) \operatorname{XOR} f(j,i) =1$的肯定不在同一个SCC里面。而由于$f(i,j) \operatorname{AND} f(j,i) =1,f(i,j) \operatorname{XOR} f(j,i) =1$中都蕴含着$f(i,j) \operatorname{OR} f(j,i) =1$,所以我们必须把所有的SCC都连成一条链。由于要让边数尽可能少,所以每个SCC一定都是单独一个点或者一个环。我们只要最小化点数大于$1$的SCC的数量就可以了。
$f(i,j) \operatorname{AND} f(j,i) =1$的点可以直接缩起来。缩完点之后,在原图中的点数为$1$的都不需要考虑;对于剩下的点,对所有的$f(i,j) \operatorname{XOR} f(j,i) =1$在$i,j$之间建一条边,问题转化成求最小的$k$,使得在这张图中可以将这些点划分成$k$个独立集。
注意到在原图中对应的点数大于$1$的点的数量不超过$\lfloor{n\over 2}\rfloor = 23$。
直接子集$dp$的复杂度是$O(3^{n\over 2})$或者$O(n^22^{n\over 2})$。
先枚举$k$,在判断的时候我们把条件放松一些:我们只要求能够选出$k$个独立集,它们的并是全集就可以了。
设$f_S$表示$S$的子集中是独立集的数量,通过容斥就可以得到:
这个$Ans$会很大,但是我们只关心$Ans$是否为$0$,用取模或者直接溢出后的结果判断就可以了。
时间复杂度$O(n2^{n\over 2})$。
LOJ2292 「THUSC 2016」成绩单
设$f_{i,j,l,r}$表示区间$[i,j]$已经删掉若干,剩下的那些元素中的最大值为$r$,最小值为$l$,删掉那若干个元素的最小代价;$g_{i,j}$表示将区间$[i,j]$全部删完的最小代价。
对于$f_{i,j,l,r}$,考虑$j$这个元素是否被删掉了:
- 如果它已经被删掉,我们枚举它是和哪些元素一起删掉的,就有:
- 否则,$j$没有被删掉,则得到
对于$g$,考虑我们是否对$[i,j]$整体进行过操作:
- 如果没有,则
- 否则
复杂度$O(n^5)$。