You may check this article on cp-algorithms.com (or OI-wiki if you prefer reading in Chinese) for more precise information and proof of complexity about SAM. Here I just want to write about another perspective to understand SAM, which I’ve learned from Huadun Hong, PKU, through Zhengruioi’s online courses on 4th, Feb, 2020.
0
We can get the suffix tree of string $S$ simply by inserting all of its suffixes into a trie (though this will involve $O(|S|^2)$ vertices). Note that:
- Each vertex in the suffix tree represents a substring of $S$ (since a substring is a prefix of a suffix of $S$). Let’s call the vertices that represent a suffix of $S$ ‘the suffix vertices’.
- The number a substring occurs in $S$ equals to the number of suffix vertices in the subtree of the corresponding vertex.
- The well-known data structure Suffix Array is actually the DFS ordering of the suffix tree. (Sort the suffix vertices by the time we discover them.)
- LCP of two suffixes is the LCA of the corresponding suffix vertices in the suffix tree.
Define:
- $len_x$: the length of the string that vertex $x$ represents, also equals to the depth of $x$ in the suffix tree.
- $fail_x$: father of $x$ in the suffix tree.
- $go_{x,ch}$: (this definition differs from traditional definition of SAM) suppose $x$ represents string $T$, then $go_{x,ch}$ is the vertex that corresponds to the string $cT$. I may write $go_{T,ch}$ for $go_{x,ch}$ or the string $go_{x,ch}$ represents for convenience in the following paragraph, so don’t get confused with it.
It seems there is some delicate contact between $go_{x,ch}$ and the suffix links in the Aho–Corasick algorithm, isn’t it? And when the suffix tree is compressed later it turns out that it’s no longer convenient to find the son of a pariticular vertex in the suffix tree, and that’s why we’ve got to maintain the array $go_{x,ch}$. Thus if we want to find the corresponding vertex of a particular string $T$, we just start from the root of the suffix tree, enumerate each character of $T$ from right to left and go to $go_{\text{current node,current character}}$.
1
In this section we’ll talk about how to construct the suffix tree and maintain $len_x, fail_x, go_{x,ch}$ by adding characters of $S$ one by one from right to left.
That is, we have already built SAM of $S$, now we wanna get SAM of $cS$ out of it.
From $S$ to $cS$, only one more suffix’s added, that’s $cS$. So first we’ll insert $cS$ into the suffix tree (remember the suffix tree here is still a trie) and maintain $len_x, fail_x$ of the newly-added vertices. We do it in the following way: we create a new vertex $u$ that represents $cS$, then we find the longest $cS[1:i]$ that occurred in $S$ and let the corresponding vertex be $v$. Then we add vertices representing $cS[1:|S|-1],cS[1:|S|-2], \cdots S[1:i+1]$ between $u$ and $v$.
Consider about the changes in $go_{x,ch}$, they can be divided into two types:
- $x$ is one of those newly-added vertices, or
- $go_{x,ch}$ is one of those newly-added vertices
Note it’s impossible to have $x$ and $go_{x,ch}$ both newly-added.
For the first type, since strings the newly-added vertices represent do not occur in $S$, so after adding $c$ at the front they won’t occur either. Then just set all $go_{x,ch}$ of the newly-added vertices to null.
For the second type, we enumerate all prefixes of $S$ that $go_{S[1:j],c}$ is null, then let $go_{S[1:j],c}$ be $cS[1:j]$. This can be done by starting from $S$ and each time jumping to the father of current node until $go_{\text{current node},ch}$ is not null.
2
Note there can be $O(|S|^2)$ vertices in the suffix tree, but number of vertices with degree greater than $2$ is at most $2|S|-1$. Then if a vertex has only one child, we compress it and its’ only-child and say the original father is ‘compressed’. Specially, because suffix vertices contain a lot of important information so we’ll never compress a suffix vertex, even if it has only one child. We call all remaining vertices after the process ‘key vertices’.
Define:
- $Z(x)$: let $Z(x)$ be the set of strings that vertices compressed into $x$ represented in the original suffix tree. Note that all strings in $Z(x)$ can be represented as one prefix of the longest string in $Z(x)$.
- $len_x$: the length of longest string in $Z(x)$.
- $fail_x$: the first key vertex we meet in the original suffix tree by starting from $x$ and continuously jumping to father of the current node.
- $go_{x,ch}$:
- An important fact is that in the original suffix tree $go_{x,ch}$ must be compressed if $x$ is compressed. To prove this let $T$ be the string $x$ represents and $cT$ be some key vertex.
- If $cT$ is a suffix vertex then $T$ should also be a suffix vertex which made $T$ impossible to be compressed.
- Then $cT$ must have two distinct children, let them be $cTx$ and $cTy$. It turns out that $T$ should also have $Tx$ and $Ty$ as its children, which meets a contradiction.
- But if $x$ is a key vertex, $go_{x,ch}$ in the original suffix tree may be compressed. In this case we let $go_{x,ch}$ be the key vertex that the original $go_{x,ch}$ has been compressed into. Thus we can ensure $\forall Y\in Z(x), cY \in Z(go_{x,c})$.
- An important fact is that in the original suffix tree $go_{x,ch}$ must be compressed if $x$ is compressed. To prove this let $T$ be the string $x$ represents and $cT$ be some key vertex.
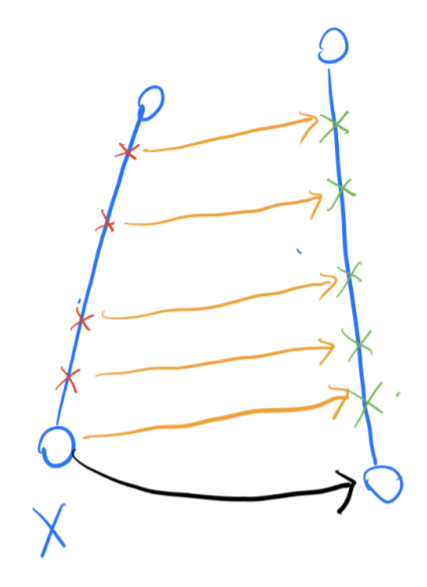
(This is a picture from Huadun Hong’s slide, representing $go_{x,c}$.)
Then consider how to build SAM with our previous algorithm. First we create a new vertex stands for $cS$.
Finding the greatest $i$ that $cS[1:i]$ occurs in $S$ is equivalent to finding the greatest $i$ that $go_{S[1:i],c}$ is not null. So we can just start from $S$ and continuously jump to $fail_{\text{current node}}$ until the current node satisfies $go_{\text{current node},c}$ is not null. Let this vertex be $Q$ and $E$ be $go_{Q,c}$.
We should set $fail_{cS}$ to a vertex that the longest string it represents is $cQ$. But note that $cQ$ may not be the longest one in $Z(E)$, if so we shall ‘decompress’ it from $E$ since we’re about to add a new child to it. Let the newly-decompressed vertex be $K$ (let $K$ be $E$ in case that $cQ$ is the longest one in $Z(E)$) and let $fail_{cS} = K$.
Now we’ll take a look at changes in $go_{x,ch}$:
- like the original $O(|S|^2)$ suffix tree, we set $go_{x,c}$ of all vertices on the chain from $S$ to $Q$ to $cS$
- and for $Q$ and $Q$’s ancestors satisfying $go_{x,c} = E$, we change $go_{x,c}$ to $K$.
Thus we’ve completed contruction of SAM.
It turns out that time complexity and memory complexity of this algorithm are both $O(|S|)$.