推荐两个带花树算法的学习资料:维基百科 Bill Yang’s blog
Q1
缩掉奇环之后,会不会存在一条交错路,和奇环相交的部分没有经过花根,成为了一条在缩掉了花之后的图中找不到的增广路?
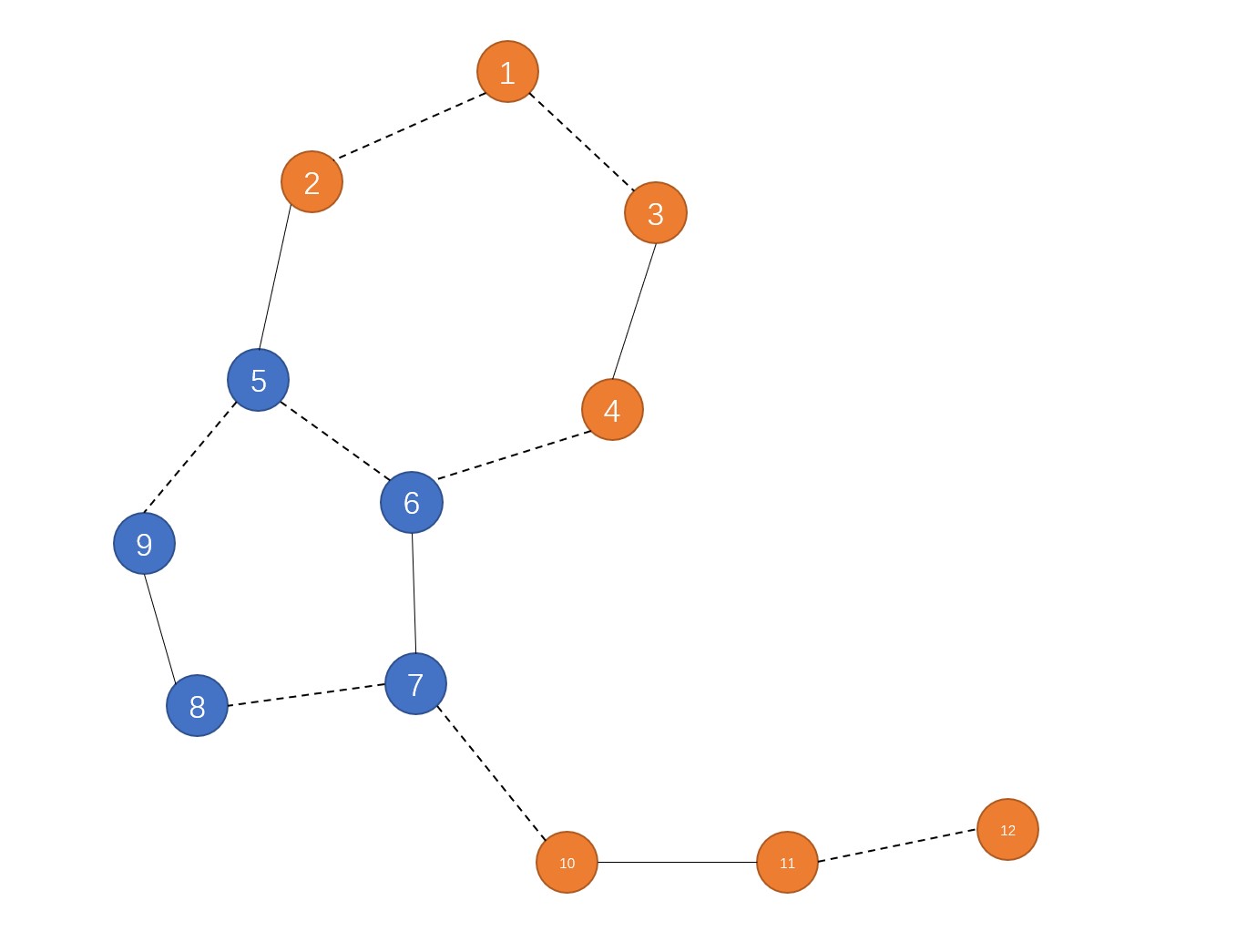
如上图,实线表示匹配边,虚线表示非匹配边,1和12是孤立点,$\{5,6,7,8,9\}$是已经缩起来的一朵花,5是花根。一条交错路是1-3-4-6-7-10-11-12,可以看到这条交错路进入花的最后一条边和离开花的第一条边都是非匹配边,无法在缩掉蓝色的花之后的图中找到。但是当我们访问到6-4这条边的时候,由于蓝色的花已经被缩起来了,就会发现$\{1,3,4,6,7,8,9,5,2\}$这个奇环并把它缩起来。所以这样的交错路是仍然能够被带花树算法找到的。
后面的问题和代码实现有关,所以先贴上我的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
|
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
#define PB push_back
#define MP make_pair
#define PII pair<int,int>
#define FIR first
#define SEC second
#define ll long long
using namespace std;
template <class T>
inline void rd(T &x) {
x=0; char c=getchar(); int f=1;
while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
const int N=510;
vector<int> G[N];
int n,fa[N],vis[N],par[N],pre[N];
queue<int> que;
int find(int x,int d=0) { if(d>n) return x; return fa[x]==x?x:fa[x]=find(fa[x],d+1); }
int LCA(int x,int y) {
static int vis[N],tim;
tim++;
x=find(x),y=find(y);
while(x) vis[x]=tim,x=find(pre[par[x]]);
while(vis[y]!=tim) y=find(pre[par[y]]);
return y;
}
void FLOWER(int x,int y,int L) {
while(find(x)!=L) {
if(fa[x]==x) fa[x]=L;
if(fa[par[x]]==par[x]) fa[par[x]]=L;
if(vis[par[x]]==2) vis[par[x]]=1,que.push(par[x]);
pre[x]=y;
y=par[x],x=pre[y];
}
}
bool bfs(int s) {
for(int i=1;i<=n;++i) fa[i]=i,vis[i]=pre[i]=0;
while(!que.empty()) que.pop();
que.push(s),vis[s]=1;
while(!que.empty()) {
int u=que.front(); que.pop();
for(int i=0;i<G[u].size();++i) {
int v=G[u][i];
if(!vis[v]) {
pre[v]=u,vis[v]=2;
if(!par[v]) {
while(v) {
int tmp=par[u];
par[v]=u,par[u]=v;
v=tmp,u=pre[v];
}
return 1;
}
vis[par[v]]=1;
que.push(par[v]);
}
else if(vis[v]==1&&find(v)!=find(u)) {
int tmp=LCA(u,v);
FLOWER(u,v,tmp),FLOWER(v,u,tmp);
}
}
}
return 0;
}
int main() {
int m; rd(n),rd(m);
for(int i=1,x,y;i<=m;++i) rd(x),rd(y),G[x].PB(y),G[y].PB(x);
int ans=0;
for(int i=1;i<=n;++i) { if(!par[i]) ans+=bfs(i); }
printf("%d\n",ans);
for(int i=1;i<=n;++i) printf("%d ",par[i]);
return 0;
}
|
Q2 (1) (2)
(1) 不能写作
1
2
| while(x) vis[x]=tim,x=pre[par[x]];
while(vis[y]!=tim) y=pre[par[y]];
|
(2) 不能写作
原因是,可能尽管我们没有进行显式的缩点,在走到奇环的时候会顺着边爬,但是在奇环嵌套偶环的时候可能会陷入死循环。
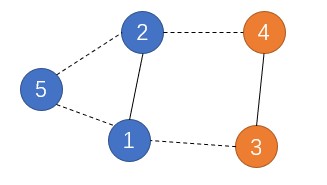
比如,上面这张图中,我们已经找到 (2,1) ,(3,4) 这两对匹配,现在开始尝试找从 5 开始的增广路。首先会找到 $\{5,1,2\}$ 这个奇环并缩起来,之后会找到 $\{5,1,3,4,2\}$ 这个奇环并缩起来,但是在缩这个奇环的过程中,
1
2
3
4
5
| while(find(x)!=L) {
pre[x]=y;
y=par[x],x=pre[y];
}
|
就会陷入(x=2, y=4) -> (x=3, y=1) -> (x=2, y=4) -> ...的死循环。
Q3 (3)
(3) 不能写作
1
2
| fa[find(x)]=L;
fa[find(par[x])]=L;
|
因为在往上爬的过程中,我们会先经过一些在花中但不是花根的点,这时候如果修改了这个花中所有的点的所属的花编号,会影响下一步用find(x)!=L判断是否已经走到了L所在的花。正确的做法是,走到花根的时候才修改花中的点所属的花编号。

