day1
A - 递增树列
题意
给定一棵有根树,定义$dis(i)$为$i$点到根经过的边数。求有多少个排列$p$,满足$\forall i \in [1,n-1), dis(lca(p_i,p_{i+1}))\le dis(lca(p_{i+1},p_{i+2}))$。
答案对$10^9+7$取模。$n\le 80$。
Sol
一个观察:从前往后考虑这个排列,一旦出现了相邻两个点的lca不为根,那么此后的点都在根的同一个子树内。而前面的相邻两个点的lca都为根等价于相邻两个点来自根的不同子树。对不是根的点考虑仅由它的子树内的点构成的排列时也有类似的结论。
设$g_{u,j}$表示以$u$为根,用了$u$子树内的$j$个点去构成一个合法的排列的方案数。则最后的答案是$g_{1,n}$。
如果排列中始终没有出现两个相邻的点lca的深度大于$u$,则可以直接用容斥原理计算。对$u$的每一个儿子枚举这个儿子的子树内选了多少个点,以及这些点中有多少对在最终排列里相邻了,并对(选了的点数)和(在同一个儿子的子树内且在排列中相邻的点对数)做背包。
如果存在相邻点lca深度大于$u$,假设其所属的儿子是$v’$,我们最后得到的排列只需满足:在lca均在$v’$之内的那一段(即$g_{v’,x}$所代表的)之前,最后一个点不属于$v’$的子树。这个仍然可以用类似于上一种情况的方法进行容斥,使得在$v’$子树内的点位于$g_{v’,x}$的那段之前的方案被减掉。在背包中再加入一维$0/1$,表示是否已经算过$v’$的贡献就可以处理这种情况。
时间复杂度$O(n^4)$。我n^5过了
B - Article
题意
定义$w(s_1,s_2)$表示$s_1,s_2$的本质不同的公共子串的数量。
定义一个字符串$t$的权值为$\sum_{i=1}^{|t|-1} w^2(s[1\cdots i],s[i+1\cdots |t|])$。
给出一个字符串$s$和正整数$k$,问将$s$划分成恰好$k$段,权值最大的那段的权值最小可以是多少。
$|S|\le 50000$,保证答案不超过$10^{18}$。
Sol
考虑如何在$O(|t|)$的时间内算出$t$的权值:对$t$建SAM,对于每个节点处理出它的出现位置的最小值和最大值;SAM上的每个节点对$i=1$到$|t|-1$时的$w$的贡献,会是一个形如$maxlen,maxlen,\cdots maxlen,maxlen-1,maxlen-2\cdots $的数列,用二次差分就可以处理。求出每个$w$之后再平方、求和即可。
首先二分答案,将问题转化成:要求每段的权值小于等于某值,问能否划分成至多$k$段。由于这个题的权值满足单调性(即一个串的权值一定不小于它的任何一个子串),所以可以直接贪心,让划分的位置尽可能靠后就可以了。
利用倍增找下一个划分点:先检查长度$2^0,2^1,\cdots$直到长度为$2^k$的串的权值大于了限制,然后再依次枚举$2^{k-1},2^{k-2}\cdots$进行倍增。假设这一次划分的段的长度的$L$,由于每一次倍增时需要计算权值的串长度大于等于$2^{k-1}$而小于$2^k$,所以找出这个划分点的复杂度是$\Theta(L\log L)$的。
总复杂度$O(|S|\log |S|\log Ans)$。
C - Travel
题意
有$n$个可重集合$S_1,S_2\cdots S_n$,你可以从每个可重集合中选出一个元素,然后用这$n$个元素构成$k$个环,要求每个环的长度都是奇数。
定义一个环的价值为,相邻两个元素的差的绝对值的最小值。特别地,一个只包含一个元素的环的价值是正无穷。
你需要最大化所有环的价值的最小值,并输出最大化的结果。
$n\le 300,|S_i|\le 5,k< n$。
Sol
Lemma 1
对于确定的$n$个已经从小到大排好序的元素$a_1,a_2,a_3\cdots a_n$,令$m={n-1\over 2}$,则它们构成的环的价值最大值是$\min \{ a_{i+m}-a_i \}$。
证明:考虑$\{a_i,a_{i+1},\cdots a_{i+m}\}$这个集合内有$m+1$个元素,集合外有$m$个元素,所以集合中必然存在一对在环中相邻的元素,所以这是答案的下界。而达到这个下界的解可以这样构造:
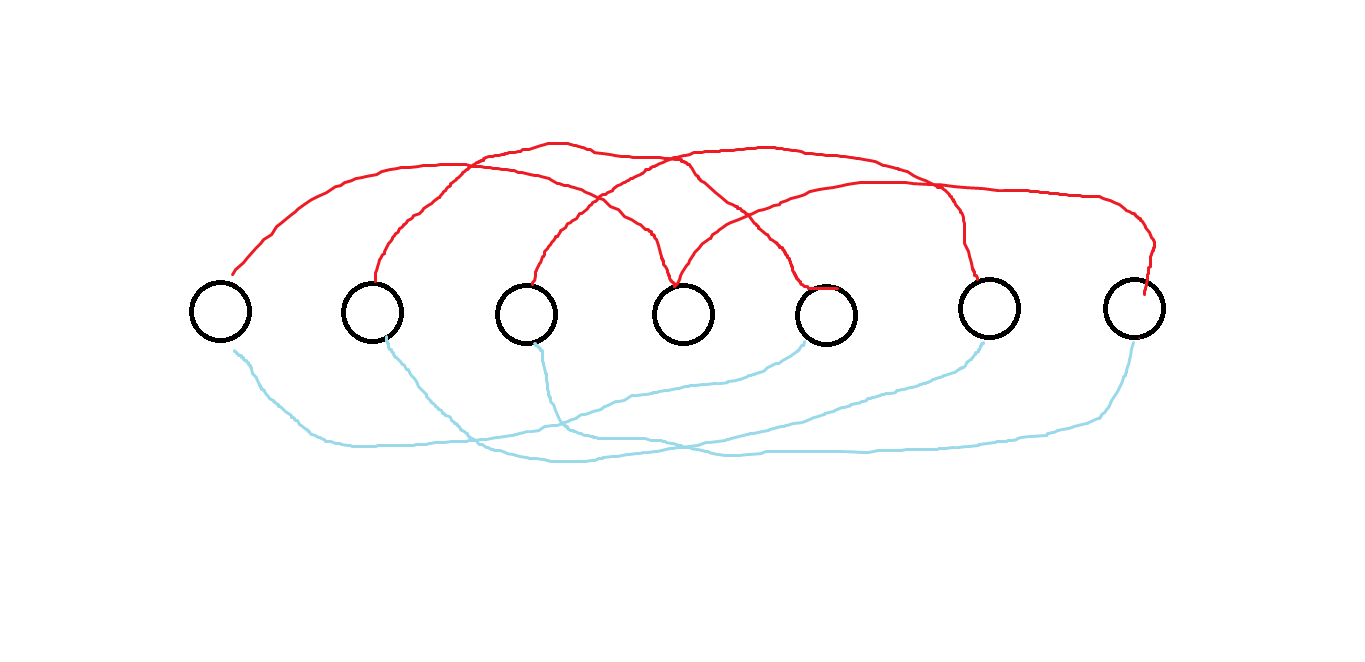
Lemma 2
最终的答案是由$k-1$个孤立的点和一个长度为$n-k+1$的环构成的。
证明:考虑现在有两个长度大于$1$的环$\{a_1,a_2\cdots a_m\}$和$\{b_1,b_2\cdots b_n\}$($a_i,b_i$随下标递增),只要证明将它们变成一个孤立点和一个环答案不会变劣就可以了。
如果某个环使用的不是上面的图片中的构造方法,将其改为图片中的构造方法不会变劣。所以下面均认为环是按照上面图片的方式构造的。
从$a$中取出一个孤立点$a_{m+1\over 2}$,得到一条一端为$a_1$,另一端为$a_m$的链。
断开$b$中的边$(b_1,b_{n+1\over 2})$或者边$(b_{n+1\over 2},b_n)$。
考虑如何将两条链拼起来。假设第一条链是的端点分别为$a,b(a< b)$,第二条链的端点为$c,d(c< d)$。若$[a,b]$与$[c,d]$没有交或者包含,则很容易构造使得拼接用的边的权值都大于等于$\min\{b-a,d-c\}$。否则一定有$b_1< a_1 \le b_{n+1\over 2} \le a_m < b_n$,此时若$b_{n+1\over 2}\ge a_{m+1\over 2}$,就连$(b_{n+1\over 2},a_1)$和$(a_m,b_1)$,否则就连$(b_{n+1\over 2},a_m)$和$(b_n,a_1)$。这样构造之后答案都不会变劣。
process
首先二分答案$w$,然后判断能否求出长度为$n-k+1$的哈密顿回路。
令$N=n-k+1$,存在长度为$N$的哈密顿回路等价于存在$N-3\over 2$对匹配和一个三元匹配。
其中$i,j$这两个集合可以匹配,当且仅当$\exists a\in S_i,b\in S_j, |a-b| \ge w$。
其中$i,j,k$这三个集合可以构成三元匹配,当且仅当$\forall x\in S_i,y\in S_j,z\in S_k, \min\{|x-y|,|y-z|,|z-x|\}\ge w$。
必要性:可以把环画成之前的图中的形式,图中红色的边为匹配边。
充分性:显然一个集合只会属于一个匹配。对于每个集合拿出一个它参与了匹配条件判定的那个元素,将所有集合按照它拿出的那个元素的大小排好序。如果它们的匹配边的连法不是之前的图中的那样,则可以进行等价的调整。然后用与前面构造相同的方法就可以构造出解。
最后是怎么求这个匹配。枚举三元匹配中元素的值为中位数的那个集合并枚举它选的元素,然后将这个集合拆成两个点,一个只能连比它小的点,另一个只能连比它大的点,然后跑一般图的最大匹配就可以了(说得就跟我会似的。。。。
day2
A - 循环数列
题意
有一个无限长的下标从$1$开始的序列,初始的时候所有在模$n$意义下等于$m$的位置的数为$1$,其余位置的数为$0$。
每一次操作会使得操作后的序列$F’_i=F_i+F_{i+1}$。
现在给出$n,m,k,pos,P$。你需要求出$k$次操作之后,$F_{pos}\pmod P$的值。
数据组数$T\le 500$,$k\le 10^9, P\le 10^7, \sum n\le 10^6, 1\le m< n, 1\le pos< n$,数据保证$P$为质数且$n\mid p-1$。
Sol
假设某个初始序列中的$1$的下标为$x$,那么它将对$F_{pos}$产生的贡献等价于:每一次可以让$x$不变或减一,操作$k$次后恰好$x=pos$的方案数。也就是${k \choose x-pos}$。
故而答案为
令$t=m-pos$,进行单位根反演:
暴力枚举$j$计算,复杂度$O(n\log k)$。
B - Matrix
题意
给出一个$n\times n$的整数矩阵$A$。
问能否求出一组置换矩阵$\{B_1,B_2\cdots B_m\}$,使得唯一存在一组非负整系数$\alpha_1,\alpha_2\cdots \alpha_m$,满足$A=\alpha_1\cdot B_1 + \alpha_2\cdot B_2+\cdots +\alpha_m\cdot B_m$。
求出一组$m\le n^2$的解或判定无解。
$n\le 50,T\le 10,A_{i,j}\le 2\times 10^7$
Sol
参考Birkhoff–von Neumann theorem。
一个$A$能够被表示出来的充分必要条件是$A$中的每一行元素的和、每一列元素的和都相同。
充分性证明:设$C$为某一行的所有元素的和。构造一个二分图,左侧有$n$个点表示每一行,右侧有$n$个点表示每一列。$(i,j)$这条边存在当且仅当$A_{i,j}>0$。用Hall定理证明这张图存在完备匹配:任选一个左边的点构成的集合$X$,考虑与他们相邻的列集合$Y$,由于$|X|\cdot C = \sum_{x\in X,y\in Y} A_{x,y} \le |Y|\cdot C$,所以有$|X|\le |Y|$,证毕。所以这张二分图一定存在完备匹配,将完备匹配对应的置换矩阵从$A$中减掉($\alpha$取匹配中的最小边权),就转化成了规模更小的问题。
上述的证明过程也描述了算法的过程。显然这样最多会用$n\times n$个置换矩阵。由于每一次都会让一个位置变成$0$,所以这一步拿出来的置换矩阵与之后拿出来的置换矩阵必然线性无关。
C - 杀蚂蚁简单版
题意
有一棵包含$n$个节点的树,每个点有一个权值$v_i$。有一只蚂蚁,如果它当前在的节点为$x$,与它相邻的点集为$\{y_1,y_2\cdots y_m\}$,则它下一秒将以${v_{y_i}\over \sum v_{y_j}}$的概率走到$y_i$这个点。蚂蚁一旦走到$1$节点就会消失。
有$q$次询问,每次询问给出$s,x,y$,你需要回答:如果蚂蚁的初始位置是在$s$,它期望有多少秒停留在$x$到$y$的最短路径上。
$n,q\le 10^5$,答案对$998244353$取模。
Sol
设$P_{x,y}$表示从$x$走到$y$的概率。
下面考虑部分分$v=u+1,s=2$的情况怎么做。设$f_i$表示$i$期望被经过多少次,那么显然有$f_2=P_{2,3}\cdot f_2+1={1\over 1-P_{2,3}}$,$f_3 = P_{2,3}f_2 + P_{4,3}\cdot f_4 $,由于出发点是$2$,终点是$1$,所以必然有$f_4P_{4,3} = f_3P_{3,4}$,所以$f_3={1\over 1-P_{3,4}}P_{2,3}f_2$。后面的可以类似的方法推导。概括一下就是,设$g_i = {1\over 1-P_{i,i+1}},h_i=P_{i-1,i}$,则$f_2 = g_2, f_i = h_ig_if_{i-1}(i>2)$。
考虑$v=u+1,s\not = 2$的情况:此时的答案等价于蚂蚁第一次走到$s-1$之前经过每个点的次数的期望 加上 以$s-1$作为出发点的时候的答案。如果限制了不能够经过$s-1$这个点,等价于让$s-1$做根,故而此时$f_s = g_s, f_i = h_ig_if_{i-1}(i>s)$。所以这种情况的答案为$\sum_{i\in [x,y]} \sum_{j=2}^s g_j\prod_{k=j+1}^i h_ig_i$。考虑如何快速计算答案:令$F_i$表示当以$2$作为起点的时候期望经过$i$的次数,那么$F_i$对答案的贡献相当于$F_i(1 + {1\over g_2h_3}+{1\over g_2g_3h_3h_4}+\cdots {1\over g_2g-_3\cdots g_{s-1}h_3h_4\cdots h_s})$。按照从小到大依次枚举$s$,当从$s-1$变成$s$的时候,相当于对于所有大于了$s$的$x$,它的贡献都增加了$F_x\cdot {1\over g_2g-_3\cdots g_{s-1}h_3h_4\cdots h_s}$,可以用线段树维护区间内的贡献和。
上面的结论推广到树仍然成立。对整棵树进行dfs遍历,进入一个点$s$的时候,就使它的子树内的点$x$都加上贡献$F_x \cdot {1\over h_sg_{fa_s}h_{fa_s}g_{fa_{fa_s}}\cdots }$,用树链剖分维护链的贡献和即可。时间复杂度$O(n\log ^2 n)$。
day3
A - 投影对称
题意
给定$n$个点,求有多少过$(0,0)$的直线,满足这$n$个点在直线上的投影为中心对称图形。
$n\le 2000$,$|x_i|,|y_i|\le 10^6$,可能会有重合的点。
Sol
假设对称中心为$P$,考虑过$P$且与$OP$垂直的直线$l$,对于一对其投影关于$P$对称的点$A,B$,它们到$l$的距离相等。故线段$AB$的中点也一定经过了$l$。枚举$1,2$这两个点匹配的另一个点是什么就可以确定$l$,然后再$O(n\log n)$检查,这样总复杂度是$O(n^3\log n)$的。
考虑由于$l$过所有点对的中点,所以$l$一定过这$n$个点的重心。因此只需要枚举$1$号点匹配的点,再考虑上重心,就可以确定$l$了。时间复杂度$O(n^2\log n)$。
有一种写法是,先对这$n$个点求一次凸包,由于凸包上的点只能和凸包上的点配对,(再加上出题人没有考虑到凸包,因此数据中凸包上的点数很少),可以将总复杂度优化到$O(Cn\log n)$,其中$C$为凸包上的点数。
B - 数圈
题意
有$n$个整数排成一个圈,初始它们为$A_1,A_2\cdots A_n$。
定义一次操作为,选择一个数$a$,将与它相邻的数加上$a$,将它变成$-a$。
问至少进行多少次操作,可以使得所有的数非负。如果办不到输出$-1$。
$n\le 10^5, -1000\le A_i \le 1000$
Sol
考虑如果是序列怎么做:观察发现,一次操作等价于交换了前缀和数组中的两个元素,所以答案就是前缀和数组的逆序对数。
而对于圈,我们定义它的广义前缀和是一个双向无限的序列$S_i(i\in \mathbb {Z})$,如1,2,-3,4的一个可能的广义前缀和是……-8,-4,-3,-1,-4,0,1,3,0,4,5,7,4,8,9,……定义它的一次交换操作为:选定一个$i$,对于所有在模$n$意义下与$i$同余的位置$x$,交换$S_x$与$S_{x-1}$。
设$sum=\sum_{i=1}^nA_i$,如果$sum< 0$显然无解,如果$sum=0$则当且仅当序列中所有元素都是$0$的时候有解,否则无解。下面只讨论$sum>0$的情况。
定义$R_i = \sum_{j>i} [ S_j< S_i]$,定义逆序对数为$R_1+R_2+\cdots R_n$。由于$sum>0$,所以$R_i$是有限的。由于$S_{x+n}=S_x+sum$,所以$R_i = R_{i+n}$。一次操作会交换所有的$S_{i+kn}$与$S_{i-1+kn}(k\in \mathbb Z)$,对于某一个$k’$,$R_{i+k’n}$只会受到交换$S_{i+k’n},S_{i-1+k’n}$的影响,所以一次操作我们恰好可以让某一个$R_i(i\in [1,n])$减掉一。所以答案就是这个逆序对数。
枚举$j-i$在模$n$意义下的取值。由于$S_{i+n}=S_i + sum$,所以$R_i = \sum_{j=1,S_{i+j}< S_i}^{n-1} \lceil{S_i-S_{i+j} \over sum}\rceil$。利用这个式子可以在$O(n^2)$的时间内解决问题。
考虑将$S_i$分解为$S_i = u_i \cdot sum +v_i(0 \le v_i < sum)$,则前面的式子转化为$\sum_{j=1,S_{i+j}< S_i}^{n-1} u_i - u_{i+j} + [v_i > v_{i+j}]$。从小到大枚举$i$并动态维护二维点集$(S_{i+j},v_{i+j})$以及点权$u_{i+j}$,可以做到$O(n\log ^ 2 n)$的复杂度。进一步观察,这个动态维护的过程中,我们每一次删除的是$((S_x,v_x),u_x)$,而加入的是$((S_{x+n},v_{x+n}) ,u_{x+n}) = (( S_x +sum, v_x), u_x +1)$。如果我们不去做这个修改,造成的影响是:对于所有的$i>x,S_i > S_x$,$R_i$会多算上$1$的贡献,这是一个二维偏序问题。不做修改的原问题也是个二维偏序问题。这样就做到了$O(n\log n)$的复杂度。
C - search
题意
交互题。有一个$n\times n$的单调矩阵(同一行的元素右边的比左边的大,同一列的元素下面的比上面的大),此外还有一个数$x$。保证矩阵内的元素以及$x$两两互不相同。有两种询问:
- 询问矩形内的某两个格子,返回它们的大小关系。
- 询问矩形内的某一个格子,返回这个格子与$x$的大小关系。
你需要回答,矩形内比$x$小的位置的个数。
$n\le 2000$,时限2s,限制询问1的次数不超过$64n$,询问2的次数不超过$34$。
Sol
一个随机算法
随机一个格子$(i,j)$,然后抠出如下图的这个轮廓线:
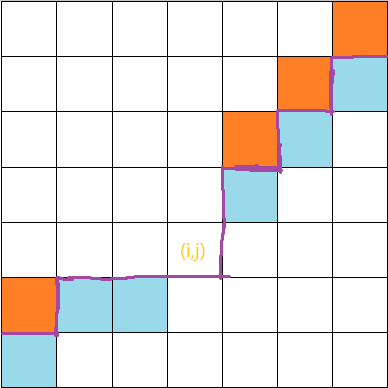
有颜色的格子是用过询问1的,橘色表示问出来比$x$小,蓝色表示问出来比$x$大。
这样抠一次,$i$行之前的,橘色格子每列至多有一个,蓝色格子每行至多有一个;$i$行之后的,橘色格子每行至多有一个,蓝色格子每列至多有一个。所以这一步会用掉至多$2n$次询问1。
比较$(i,j)$与$x$的大小关系。若$(i,j) < x$,则轮廓线上方的全部都$< x$,可以记入贡献之后删掉;否则,$(i,j) > x$,则轮廓线下方的也全部$> x$,可以删掉。
期望只需要进行$O(\log n)$次上述操作,就可以结束程序。
day4
A - xor
题意
给定$n,d$,求
其中$\oplus$表示按位异或。
$n< 2^{30},d\le 100000$。
Sol
部分分:$d\le 10$
下面是一个和正解毫无关系的暴力。
通过数位$dp$单独对二进制每一位进行考虑。考虑怎么算答案,设$p_i$表示第$i$位是$0$还是$1$,由多项式乘法的组合意义可得:
在$dp$状态中加入一维表示$l_1 + l_2 +\cdots l_{cur_len}$,就可以在$O(\log n \cdot 2^3 \cdot d^2)$的时间内解决问题。
正解
枚举$x,y,z$最高的和$n$不同的一位,假设为$a,b,c$。不失一般性地令$a\le b\le c$。$x\oplus y\oplus z$可能取到的数,满足$c$以上的位全部与$n$相同,$c$位为$0$且$n$的$c$位为$1$,$c$以下的位任意。考虑末$c$位取到某个$L\in [0,2^c)$的方案数,发现我们可以先让$x$的末$a$位、$y$的末$b$位随便取,然后根据$x,y$和$L$唯一地确定$z$的末$c$位,故而方案数为$2^{a+b}$。这也就是说,枚举完$a,b,c$之后,$x\oplus y\oplus z$的每一个可能的取值出现的方案数是一样的。所以只需要求出所有的可能取到的数的$d$次方的和就可以了。可能取到的数形成了一个连续的区间,是经典的自然数幂和问题。直接枚举$a,b,c$计算的复杂度为$O(d\log ^ 3 n)$,观察发现可取到的数形成的区间只与$\max\{ a,b,c\}$有关,所以只需要算$\log n$次自然数幂和就可以了,复杂度$O(d\log n + \log^3 n)$。
B - N门问题
题意
$N$扇门中有一扇门是有奖的。初始的时候$A$认为所有门有奖的概率是相等的。每一轮,$A$会在有奖概率最大的门中随机选择一扇,然后主持人会从没有被$A$选择且没有奖的所有门中随机选择一扇门打开。进行到第$N-1$轮时,$A$的选择就是他的最终选择。
现在你来当主持人,你可以决定(而不是随机地)每一次打开哪一扇没有被$A$选择且没有奖的门,问$A$最终选择的门后面有奖的概率最小是多少。假定$A$不知道你是托儿,即$A$仍然认为你是在随机选择门。
$N\le 10^{18}$
Sol
假设在某一轮,$n$个门后面有奖且主持人做出这样的选择的概率(贝叶斯公式中的$P(B\mid A)$)分别是$p_1,p_2,\cdots p_n$。
假设$A$选择的门是$x$,而你打开的门是$y$,则:
下面将证明,在某一轮$\forall k \not = x,y, p’_x < p’_k$。考虑归纳。对于第一轮显然成立。假设现在是第$t$轮,还剩下$n$扇门没有开。由于$p’_k(k\not=x,y)$之间的大小关系由$p_k$决定,所以只需要考虑$p_k$中的最小值$p_q$乘上$1\over n-2$与$p_x \cdot {1\over n-1}$的大小关系。而由于归纳,$p_q$在上一轮中是最大的,用$\{ p’’_i\}$表示上一轮的数,则$p’_q = p’’_q \cdot {1\over (n-2)(n-2)}$,而$p’_x = p’’_x \cdot{ 1\over (n-3)(n-1)}$,所以可以推出。。。什么也推不出来。
不知道怎么证明的,$N>10$的时候答案为$0$,$N\le 10$的时候直接搜索。
C - 区间匹配
题意
有两个长度为$n$的序列$a[1\cdots n],b[1\cdots n]$和两个非负整数$la,lb(lb \le la)$,你需要求出一个$1$到$n$的排列$\{p\}$,使得对于所有$i$都有$a[i] \le b[p[i]] \le a[i] + la$,在此基础上你需要最大化满足$a[i] + lb \ge b[p[i]]$的$i$的数量,并输出最大化的结果。
$n\le 500000$,$a[i],b[i],la,lb\le 500000$,且保证存在合法的$p$。
Sol
考虑这样的一种贪心:从右到左考虑每一个$a$的元素,确定与它匹配的$b[p[i]]$。设现在还没有匹配过的元素中,最靠右的一个是$b[x]$,以及最靠右且满足$a[i] \le b[y] \le a[i]+lb$的是$b[y]$。如果让$a[i]$匹配上$b[y]$,剩下的点仍然存在合法的匹配,则让$a[i]$匹配$b[y]$;否则让$a[i]$匹配$b[x]$。
正确性证明:假设这样得到的不是最优解,考虑最优匹配中第一个与这样求出来的匹配不同的位置$i$,如果$i$匹配的既不是$x$也不是$y$,将$i$匹配的改成$x$或者$y$,答案一定不会变劣;假设最优匹配中$i$匹配了$y$,则意味着让$i$匹配$y$之后仍然存在完备匹配,所以我们的贪心策略也会让$i$匹配$y$;而如果最优匹配中$i$匹配了$x$,我们的贪心策略让$i$匹配了$y$,设我们的贪心策略中匹配了$x$的是$q_x$(显然$q_x$对答案没有贡献),而最优策略中$q_x$匹配$z$,则有两种情况:
- $z\le y$,则$q_x,z$这一对有可能对答案产生了贡献,此时我们将最优决策改为$x$匹配$q_x$,$i$匹配$y$,显然是不会变劣的。
- $z> y$,则$q_x,z$这一对一定对答案没有贡献。继续考虑$q_z$和最优策略中$q_z$所匹配的$w$,若$w\le y$就改成$q_x$匹配$x$,$q_z$匹配$z$,$i$匹配$y$,答案不会变劣,因为用到的$y$的右侧的点的集合是一样的,并且用到的$y$的左侧的点(从$w$变成了$y$)没有向左移,而已经确定了的匹配的贡献也没有变小;否则,继续考虑$q_w$直到匹配的点在$y$的左侧。
直接检查是否存在完备匹配是$O(n\log n)$的(排序+贪心)。由Hall定理可得,存在完备匹配的条件是,不存在$z$使得$\sum_{i} [b[i] \ge z] > \sum_{j} [a[j] + la \ge z]$。用线段树维护每个$z$的$\sum_{i} [b[i] \ge z] - \sum_{j} [a[j] + la \ge z]$以及区间最小值,并支持区间$+1/-1$,即可在$O(n\log n)$的时间内解决问题。