day 1

A - 排列

题意

有一个$\{1,2,\cdots n\}$的排列$P$。按照字典序从小到大的顺序，依次连接所有字典序不大于$P$的$\{1,2,\cdots n\}$的排列（例如$[2,1,3]$得到的是$[1,2,3,1,3,2,2,1,3]$）。

求得到的序列的本质不同的子序列的数量。$n\le 50$，答案对$998244353$取模。

Sol

我们设$A_S[i][j]$表示满足下列条件的子序列$t$的个数：

$t$的开头是字符$i$，结尾是字符$j$
$t$不是$S$的子序列
$t$删掉最后一个字符之后是$S$的子序列

用$S+T$表示将$T$拼在$S$的后面得到的字符串，则$A_{S+T}[i][j] = \sum_k A_S[i][k] \times A_T[k][j]$。

令$P_i$表示最小的$i!$个排列首尾相接得到的序列。$A_{P_1}$可以直接求得。

考虑如何求得$A_{P_i}$求得$A_{P_{i+1}}$，发现$P_{i+1}$的可以分成$i+1$段，每一段的长度为$i!$，并且每一段与$P_i$的构成是相同的，所以每一段的$A$可以通过$A_{P_i}$交换一些行列得到。

预处理出所有的$A_{P_i}$之后，原序列可以被拆分成若干个极长的段，满足每一段是将末$i$个数进行全排列，将得到的排列按照字典序从小到大拼起来得到的。而这一段的$A$一定能通过$A_{P_i}$交换一些行列得到。

B - 火山哥与集合

题意

初始有$n$个集合，第$i$个集合只包含$1$个元素$a_i$。

每一次操作会随机选择两个集合合并。

定义一个集合的价值为这个集合中最大值与最小值的差的平方。定义$f(k)$为进行$n-k$次操作后，所有集合的价值的和的期望。

给出$l,r$，求$\sum_{k\in [l,r]} f(k)^{97376} \pmod {998244353}$

$n\le 2\times 10^5,1\le l\le r\le n,a_i < 998244353$

Sol

设$g(t,k)$表示若最终合并为$k$个集合，某个大小为$t$的集合出现的概率。设$h(i)$表示所有大小为$i$的集合的$( \max - \min )^2$的和。则$f(k)=\sum_{i=1}^n h(i) \cdot g(i,k)$。

将$a$从小到大排序后，可以得到$h(i) = \sum_{l\le r} (a_r-a_l)^2 \cdot {r-l-1\choose i-2}$。先对于每一个$t$算出$\sum_{t=r-l} (a_r-a_l)^2$，然后再算$h(i)$。这两步都可以用NTT做到$O(n\log n)$。

将$n$个集合恰好合并成$k$个的方案数是$\prod_{i=k+1}^n {i\choose 2}$（即第$i$次合并的时候，共有$n-i+1$个集合，所以合并的方案数是$n-i+1\choose 2$）。令$D(n)=\prod_{i=2}^n {i\choose 2}$。

则$g(i,k) = {n-k\choose i-1} \cdot D(i) \cdot {D(n-i)\over D(k-1)} \over {D(n)\over D(k)} = {n-k\choose i-1} \cdot {k\choose 2} \cdot D(i) \cdot D(n-i) \cdot{1\over D(n)}$

则$f(k) = \sum_i h(i)g(i,k)
={k\choose 2} \cdot {1\over D(n)}\sum_i h(i)D(i)D(n-i)\cdot {n-k\choose i-1}$

这是个卷积的形式，可以NTT优化。

C - 数论结构

题意

有一个$n\times m$的矩阵，初始所有位置的数为$0$。先进行$q_1$次修改操作，给出参数$s,l,r,x$，表示给所有满足$\gcd(s,a)=1,b\in [l,r]$的格子$(a,b)$加上$x$。然后进行$q_2$次询问操作，每次给出$(s,l,r)$，你需要回答所有满足$\gcd(s,a)=1,b\in[l,r]$的格子$(a,b)$的和。

保证修改和询问的$s$随机生成。

$n,q_1\le 50000, m,q_2\le 200000,1\le l\le r\le m, 1\le s\le n$

Sol

考虑所有修改$(s_i,l_i,r_i,x_i)$对询问$(s,l,r)$的贡献。

设$Q_d$为所有满足$d\mid s_i$的$i$构成的集合。

$\begin{aligned} \sum_{i=1}^{q_1} card( [ l_i,r_i]\cap [l,r]) x_i \cdot \sum_{j=1}^n [(s_i,j)=1 ] [(s,j)=1] \\ =\sum_{i=1}^{q_1} card( [ l_i,r_i]\cap [l,r]) x_i \cdot \sum_{j=1}^n ( \sum_{d_1\mid (s_i,j)}\mu (d_1) \sum_{d_2\mid (s,j)} \mu(d_2))\\ =\sum_{d_2\mid s} \mu(d_2) \sum_{d_1=1}^{n} \mu(d_1) \lfloor { n\over lcm(d_1,d_2)} \rfloor \cdot \sum_{i\in Q_{d_1}} card( [ l_i,r_i]\cap [l,r]) x_i \end{aligned}$

考虑枚举$d_1,d_2$的最大公约数$D$，令$t_1 = {d_1 \over D}, t_2 = {d_2 \over D}$：

$\begin{aligned} 原式 = \sum_{D\mid s} \sum_{t_2 \mid {s\over D}} \mu(t_2D) \sum_{t_1=1}^{\lfloor {n\over D} \rfloor}\mu(t_1D) \lfloor {n\over t_1t_2D} \rfloor [(t_1,t_2)=1] \sum_{i\in Q_{t_1D}} card( [ l_i,r_i]\cap [l,r]) x_i\\ = \sum_{D\mid s} \sum_{t_2 \mid {s\over D}} \mu(t_2D) \sum_{t_1=1}^{\lfloor {n\over D} \rfloor}\mu(t_1D) \lfloor {n\over t_1t_2D} \rfloor \sum_{d\mid (t_1,t_2)} \mu(d)\sum_{i\in Q_{t_1D}} card( [ l_i,r_i]\cap [l,r]) x_i\\ \end{aligned}$

令$T=D\cdot d, u_1 = {t_1\over d} = {d_1 \over T},u_2 = {t_2\over d} = {d_2\over T}$，得到

$原式 = \sum_{T\mid s} \sum_{d\mid T} \mu(d) \sum_{u_2 \mid {s\over T}} \mu(u_2T) \sum_{u_1=1}^{\lfloor {n\over T}\rfloor} \mu(u_1T) \lfloor {n\over u_1u_2dT}\rfloor \sum_{i\in Q_{u_1T}} card( [ l_i,r_i]\cap [l,r]) x_i$

在最外层枚举$T$，然后考虑所有的$Q_T$对$A_T$（表示所有$T\mid s_i$的询问）的贡献。

维护一个二维的矩阵。对于每个修改，枚举所有$d\mid T, u_1\in [1,\lfloor {n\over T}\rfloor ]$，然后对于每一个$i \in Q_{u_1T}$把第$\lfloor {n\over u_1dT}\rfloor$行的区间$[l_i,r_i]$加上$x_i \cdot \mu(u_1T) \cdot \mu(d)$。对于每一个询问，枚举所有的$u_2$，然后枚举$t$，则所有满足$\lfloor {j\over u_2} \rfloor = t$的$j$形成一个连续的区间，查这个区间的所有行的$[l_i,r_i]$的元素的和，乘上$t$加入答案中。

修改的复杂度：

$\begin{aligned} \sum_{T=1}^n \sum_{d\mid T} \sum_{u_1=1}^{\lfloor {n\over T}\rfloor} |Q_{u_1T}|\\ = \sum_{T=1}^n \sum_{d\mid T} \sum_{u_1=1}^{\lfloor {n\over T}\rfloor} {q_1\over u_1T} \end{aligned}$

因为$n,q_1$同级，用$n$换掉$q_1$：

$\begin{aligned} 原式= \sum_{T=1}^n \sum_{d\mid T} {n\over T} \log {n\over T} \\ \le \sum_{T=1}^n \sum_{d\mid T} {n\over T} \log n \\ =\sum_{d=1}^n \sum_{T'=1}^{\lfloor {n\over d}\rfloor} {n\over dT'} \log n \\ =\sum_{d=1}^n {n\over d} \log {n\over d} \log n \\ \le \sum_{d=1}^n {n\over d} \log^2 n \\ = n\log^3 n \end{aligned}$

处理前缀和的复杂度是矩阵的大小。矩阵的行数是$O(\sqrt {n\over T})$的，尽管矩阵的列数是$n$，但是其中只有$|Q_T|+|A_T|$列有用，所以复杂度是：

$\begin{aligned} \sum_{T=1}^n \sqrt {n\over T} \cdot {q_1+q_2\over T}\\ {\sqrt n (q_1+q_2) }\sum_{T=1}^n {1\over T^{1.5}} \end{aligned}$

后面部分

$\begin{aligned} \sum_{T=1}^{n} {1\over T^{1.5}} \\ \int_{1}^n T^{-1.5} dT \\ = - {1\over 0.5} n^{-0.5} + {1\over 0.5}1^{-0.5} + C\\ = n^{-0.5} \cdot 0 + C \\ = O(1) \end{aligned}$

所以这一步的复杂度是$O((q_1+q_2)\sqrt n)$。

离散化那$|Q_T|+|A_T|$列的复杂度是$\sum_{T=1}^n ( |Q_T|+|A_T| )\log n = O(q_2\log ^2 n)$。

询问的复杂度：对于某一个$u_2$，我们会枚举到的$t$一定有$\lfloor {n\over u_1u_2dT} \rfloor = \lfloor { \lfloor {n\over u_2T}\rfloor \over x} \rfloor$的形式，所以，这样的$t$只有$O(\sqrt {n\over u_2T})$个。

$\begin{aligned} \sum_{T=1}^n \sum_{j\in A_{T}} \sum_{u_2 \mid {s_j\over T}} \sqrt {n\over u_2T} \\ = \sqrt n\sum_{u_2=1}^n \sqrt { 1 \over u_2 } \sum_{T=1}^{n\over u_2 } \sqrt{1\over T} |A_{u_2T}| \\ = \sqrt n \sum_{u_2=1}^n \sqrt { 1 \over u_2} \sum_{T=1}^{n\over u_2 } \sqrt{1\over T} {q_2\over u_2T}\\ = \sqrt nq_2 \sum_{u_1=1}^n u_2^{-1.5}\sum_{T=1}^{n\over u_2} T^{-1.5} \\ = O(\sqrt nq_2) \end{aligned}$

总时间复杂度$O(n\log^3 n +q_2\sqrt n)$。

day 2

A - 火山哥的打铁传说

题意

进攻方有两种鱼：小鱼和剧毒鱼。防御方有两种鱼，圣盾鱼和大鱼。每一回合，进攻方会选择自己的一条鱼，然后让它与防御方的某一条鱼战斗。战斗遵循如下规则：

如果圣盾鱼与任意一种鱼战斗，它会变成一条大鱼。
如果大鱼和剧毒鱼战斗，它会消失。如果大鱼和小鱼战斗，大鱼不会消失。

现在你知道了进攻方前$n$个回合会选择自己的哪种鱼。有$q$次询问，每次询问给出$X$,$K$，你需要回答，如果防御方有$X$条大鱼，进攻方进行前$K$个回合，防御方最多能有多少条圣盾鱼，使得进攻方可以让防御方所有的鱼都消失。

$n,q\le 4\times 10^5$

输入格式

第一行两个整数$n,q$。

第二行一个长度为$n$的字符串$s$，$s_i$为1表示第$i$个回合进攻方出剧毒鱼，$s_i$为0则表示第$i$个回合进攻方出小鱼。

接下来$q$行，每行两个整数$X,K(1\le K\le n)$，表示第$i$次询问。

输出格式

对于每个询问，输出一行一个整数表示答案。如果圣盾鱼个数为$0$的时候进攻方仍不能消灭所有的鱼，输出$-1$。

Sol

问题等价于：我方先出$X$条小鱼，然后再进行前$K$个回合，最多能消灭掉多少条对方的圣盾鱼。假设答案为$y$，若$y< x$输出$-1$，否则输出$y-x$。

转化成求出尽可能多的小鱼和剧毒鱼的匹配（要求小鱼在前面），答案就是这个匹配数加上剩下的剧毒鱼的数量的一半下取整。

如果只有一次询问，可以直接贪心：从前往后考虑，用一个变量记录下前面的还没有匹配过的小鱼，遇到剧毒鱼的时候如果前面没有匹配的小鱼数量不为$0$就让它匹配。

从前往后贪心和从后往前贪心得到的结果显然是一样的。先从前往后贪心，求出每一个前缀能够得到的最大的匹配数。询问的时候增加的$X$条小鱼所能够增加的匹配数，是前$K$个回合中还没有匹配的剧毒鱼数量和$X$的较小值。

时间复杂度$O(n+q)$。

B - 火山哥的分式

题意

定义如下的表示一个分式的方式：给出一个长度为$l+1$的序列和长度为$l$的排列，排列中的第$i$个数代表了从上往下第$i$条分数线的长度，序列中的第$i$个元素代表了分式从上往下的第$i$个元素。例如，序列$\{ a,b,c\}$和排列$\{2,1\}$所对应的分式是：

${a\over {b\over c}}$

越短的分数线，运算的优先级越高。

现在有一个长度为$n+1$的序列$a$和长度为$n$的$\{1,2,\cdots n\}$的排列。有$q$次询问，每次询问给出$l,r$，你需要求出$a[l-1\cdots r]$和$p[l\cdots r]$对应的分式的值对$998244353$取模的结果。

$n,q\le 5\times 10^5, 0< a_i < 998244353$

Sol

单独考虑每一个元素对答案的贡献，这个贡献要么是它本身，要么是它的逆元；找出这个元素左边第一条分数线，然后找出这条分数线的左边第一条比它长的分数线，然后找左边第一条比它长的分数线……直到找到的分数线位置超出了区间，这期间找到过的分数线的个数如果是奇数那么这个数的贡献就是它的逆元，否则就是它本身。

将询问离线下来，然后从左到右扫描整个序列，并用单调栈维护已经扫过的元素（栈顶是最后加入的分数线，栈中的每一个元素的下面是它左边的第一个比它长的分数线）。扫到$r$的时候，我们分两部分求$l$的答案：一部分是仍然在栈中的元素的贡献，对于下标在$l$之后且在栈中的元素，分别查出下标为奇数和偶数的所有元素的乘积就可以得到答案；一部分是已经出栈了的元素的贡献，我们在元素出栈的时候维护。把出栈的元素的贡献分为两部分：一部分是$l$小于出栈后的栈顶的，直接让出栈后的栈顶的权值乘等于当前的栈顶的权值的逆元就可以了；另一部分是$l$在出栈后的栈顶和当前的栈顶之间的，这些$l$形成连续的一段区间且当前出栈的元素对它们的贡献是相同的，用线段树维护即可。

时间复杂度$O((n+q)\log n)$。

C - 最小割

题意

对于一张边带权的无向图，定义$s$与$t$的最小割$f(s,t)$：求一个边集$E$使得删去$E$中的边之后$s,t$不连通且$E$中的边的边权和最小，$E$的边权和即为$f(s,t)$。

现在给出了一张$n$个点$m$条边的图，其中第$i$条边连接$x_i$和$y_i$，边权为$w_i(w_i\le 10^4)$。然后可怜又往图中加了$n$条边，第$i$条边连接$i$和$i\pmod n + 1$，每条边的边权都是$10^9$。

可怜希望你求出$\sum_{s=1}^{n-1} \sum_{t=s+1}^n f(s,t) \pmod {998244353}$。

$n\le 7000,m\le 10^5$

Sol

由于所有边的权值和最多为$10^9$，所以边权为$10^9$的边肯定恰好被割两条，把原图划分成两条链，然后将链之间的边割掉。

利用二维前缀和可以在$O(n^2)$的时间内求出选择割某两条边，其它需要割掉的边的权值和。

对于$s,t$，我们要求割的一条边在$s,s+1,\cdots ,t-1,t$之间，另一条不在这些点之间。

可能的方案形成了这样的区域（横坐标代表一条边的位置，纵坐标代表另一条边的位置）：

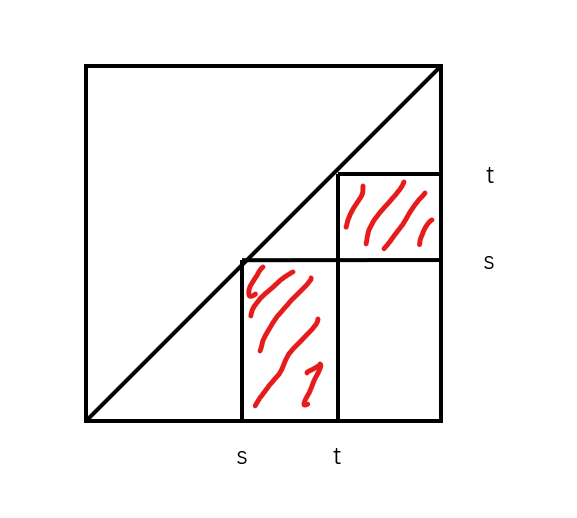
第一种：求出每一列的后缀最小，然后对于第$s$行，求出从第$s$列开始的前缀最小。

第二种：求出每一行的后缀最小，然后对于第$t$列，求出从第$t$行开始的前缀最小。

总时间复杂度$O(n^2 + m)$。