三角函数及其反函数的导数整理+证明

定义-三角函数

函数名称	符号
正弦	$\sin \theta$
余弦	$\cos \theta$
正切	$\tan \theta$
余切	$\cot \theta$
正割	$\sec \theta = \frac{1}{\cos \theta}$
余割	$\csc \theta = \frac{1}{\sin \theta}$

其中

$\begin{aligned} \cot \theta &= \frac{1}{\tan \theta}\\ \sec \theta &= \frac{1}{\cos \theta}\\ \csc \theta &= \frac{1}{\sin \theta} \end{aligned}$

求导-三角函数

几个非常有用的结论

a) $\lim_{\theta\to 0} \frac{\sin \theta}{\theta} = 1$

1. $\cos \theta < \frac{\sin \theta}{\theta}$

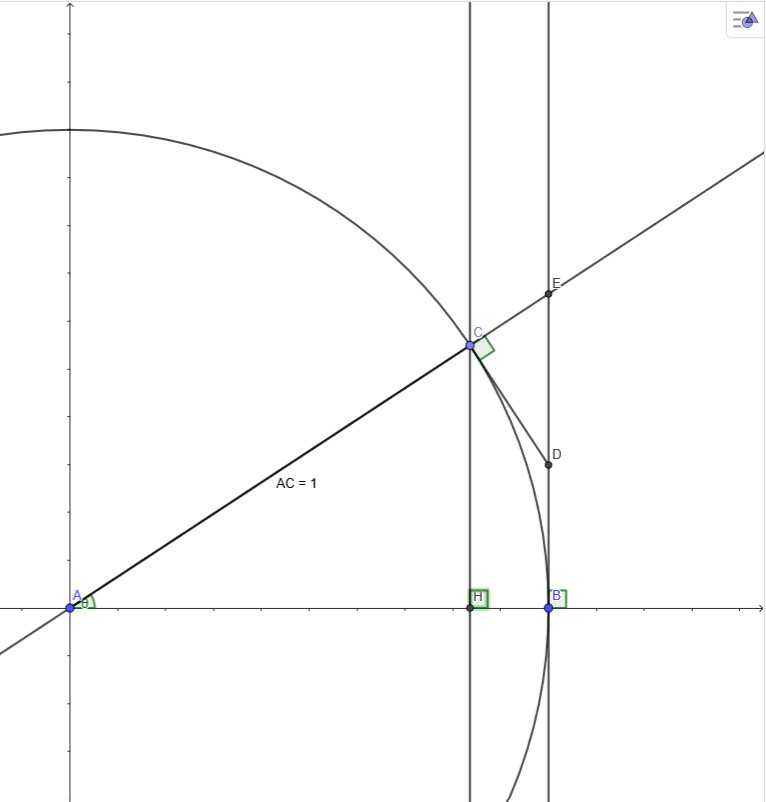
如图， $\odot A$ 是单位圆， $AC$ 为一条过 $A$ 的射线，它与 $x$ 轴正方向的夹角为 $\theta$ 。则：

$\theta = \overset{\large\frown}{BC}$（由弧度制的定义得)
$\sin \theta = CH$
$\tan \theta = EB$

于是

$\begin{aligned} \theta = \overset{\large\frown}{BC}\\ < CD+DB\\ < ED + DB\\ = EB = \tan \theta\\ \therefore \theta < \tan \theta\\ \Rightarrow \theta < \frac{\sin \theta}{\cos \theta}\\ \Rightarrow \cos \theta < \frac{\sin \theta}{\theta} \end{aligned}$

2. $\frac{\sin\theta}{\theta} < 1$

从上面的图可以看出来：

$\begin{aligned} \sin \theta &= CH < BC < \overset{\large\frown}{BC} = \theta\\ \therefore \sin \theta &< \theta\\ \Rightarrow \frac{\sin \theta}{\theta} &< 1 \end{aligned}$

3. final proof

因为

$\begin{aligned} \cos \theta < \frac{\sin \theta}{\theta} < 1\\ \lim_{\theta \to 0} \cos \theta = 1\\ \lim_{\theta \to 0} 1 = 1 \end{aligned}$

由夹逼定理知

$\begin{aligned} \lim_{\theta\to 0} \frac{\sin \theta}{\theta} = 1 \end{aligned}$

b) $\lim_{\theta\to 0} \frac{\cos \theta -1 }{\theta} = 0$

$\begin{aligned} &\lim_{\theta\to 0} \frac{\cos \theta -1 }{\theta}\\ =& \lim_{\theta\to 0} \frac{\cos \theta - 1}{\theta} \cdot \frac{\cos \theta + 1}{\cos \theta + 1}\\ =& \lim_{\theta\to 0} \frac{-\sin^2 \theta}{\theta(\cos \theta + 1)}\\ =& - \lim_{\theta\to 0} \frac{\sin \theta}{\theta} \cdot \lim_{\theta \to 0} \frac{\sin \theta}{\cos \theta + 1}\\ =& - 1 \cdot \frac{0}{1+1} = 0 \end{aligned}$

c) $\lim_{x\to 0} \frac{1-\cos x }{\frac{x^2}{2}} = 1$

$\begin{aligned} & \lim_{x\to 0} \frac{1-\cos x}{\frac{x^2}{2}}\\ = & 2\lim_{x\to 0} \frac{1-\cos x}{x^2}\\ = & 2\lim_{x\to 0} \frac{(1-\cos x)(1+\cos x)}{x^2(\cos x +1)}\\ = & 2\lim_{x\to 0} \frac{\sin^2 x}{x^2(\cos x +1)}\\ = & 2\lim_{x\to 0} \left(\frac{\sin x}{x}\right)^2 \lim_{x\to 0} \frac{1}{1+\cos x}\\ = & 2 \cdot 1 \cdot \frac{1}{2}\\ = & 1 \end{aligned}$

$(\sin x)’ = \cos x$

$\begin{aligned} &(\sin x)'\\ =& \lim_{h\to 0} \frac{\sin (x+h) - \sin x}{h}\\ =& \lim_{h\to 0} \frac{\sin x \cos h + \sin h \cos x - \sin x}{h}\\ =& \sin x \cdot \lim_{h\to 0} \frac{ \cos h - 1}{h} + \cos x\cdot \lim_{h\to 0} \frac{\sin h}{h}\\ =& \cos x \end{aligned}$

$(\cos x)’ = -\sin x$

$\begin{aligned} &(\cos x)'\\ =& \lim_{h\to 0} \frac{\cos(x+h)-\cos x}{h}\\ =& \lim_{h\to 0} \frac{\cos x\cos h - \sin x \sin h - \cos x}{h}\\ =& \cos x \cdot \lim_{h\to 0} \frac{\cos h - 1}{h} - \sin x \lim_{h\to 0} \frac{\sin h}{h}\\ =& - \sin x \end{aligned}$

$(\tan x)’ = \sec^2 x$

$\begin{aligned} &(\tan x)'\\ =& (\frac{\sin x}{\cos x})'\\ =& \frac{\cos^2 x + \sin^2 x}{\cos^2 x}\\ =& \sec^2 x \end{aligned}$

$(\cot x)’ = -\csc^2 x$

$\begin{aligned} &(\cot x)'\\ =& (\frac{\cos x}{\sin x})'\\ =& \frac{-\sin^2 x - \cos^2 x}{\sin^2 x}\\ =& - \csc^2 x \end{aligned}$

$(\sec x)’ = \sec x \cdot \tan x$

$\begin{aligned} &(\sec x)'\\ =& (\frac{1}{\cos x})'\\ =& \frac{\cos x \cdot 0 + \sin x \cdot 1}{\cos ^ 2 x}\\ =& \sec x\cdot \tan x \end{aligned}$

$(\csc x)’ = -\csc x \cot x$

$\begin{aligned} &(\csc x)'\\ =& (\frac{1}{\sin x})'\\ =& \frac{\sin x \cdot 0 - \cos x \cdot 1}{\sin^2 x}\\ =& - \csc x\cdot \cot x \end{aligned}$

求导-反三角函数

$(\sin^{-1} x)’ = \frac{1}{\sqrt {1-x^2}}$

$\begin{aligned} \sin y &= x\\ \cos y \cdot y'&= 1\\ y' &= \frac{1}{\cos \left(\sin^{-1} x\right)}\\ y' &= \frac{1}{\sqrt{1-x^2}} \end{aligned}$

$(\cos^{-1} x)’ = -\frac{1}{\sqrt{1-x^2}}$

$\begin{aligned} \cos y &= x\\ -\sin y \cdot y' &= 1\\ y' &= \frac{1}{-\sin \left(\cos^{-1} x\right)}\\ y' &= - \frac{1}{\sqrt{1-x^2}} \end{aligned}$

$(\tan^{-1} x)’ = \frac{1}{1+x^2}$

$\begin{aligned} \tan y &= x\\ \sec^2 y \cdot y' &=1\\ y' &= \frac{1}{\sec^2\left(\tan^{-1}x\right)}\\ \because \sec^2 \theta - 1 &= \left(\sec \theta \cdot \sqrt{1-\frac{1}{\sec^2 \theta }}\right)^2 = \tan^2 \theta\\ \therefore y'&= \frac{1}{1+x^2} \end{aligned}$

$(\cot^{-1} x)’ = - \frac{1}{1+x^2}$

$\begin{aligned} \cot y &= x\\ -\csc^2 y \cdot y' &= 1\\ y' &= -\frac{1}{\csc^2 \left( \cot^{-1} x\right)}\\ \because \csc^2 \theta -1 &= \left( \csc x \sqrt{1-\frac{1}{\csc^2 x} }\right)^2 = \cot^2 x\\ y' &= -\frac{1}{x^2+1} \end{aligned}$

$(\sec^{-1} x)’ = \frac{1}{x\sqrt{x^2 - 1}}$

$\begin{aligned} \sec y &= x\\ \sec y' \cdot \tan y' \cdot y' &= 1\\ y' &= \frac{1}{\sec\left(\sec^{-1}{x}\right) \tan \left( \sec^{-1} x\right)}\\ y' &= \frac{1}{x\sqrt{x^2-1}} \end{aligned}$

$(\csc^{-1} x)’ = - \frac{1}{x\sqrt{x^2 - 1}}$

$\begin{aligned} \csc y &= x\\ -\csc y' \cdot \cot y' \cdot y' &= 1\\ y' &= -\frac{1}{\csc\left(\csc^{-1}{x}\right) \cot \left(\csc^{-1} x\right)}\\ y' &= \frac{1}{x\sqrt{x^2-1}} \end{aligned}$