Sol
考虑给一个第一行确定的矩形涂色的方案数:
- 第一行是红蓝交错的(RBRBRBR…或者BRBRBRB…)
- 那么,接下来的每一行都有恰好两种选择,RBRBR…或者BRBRBR…,方案数是 $2^{n-1}$
- 第一行存在两个相邻的位置颜色相同
- 显然在第二行中,那两个位置的颜色也是相同的;以此类推,这个矩形中的每一行都会有两个相邻的位置颜色相同
- 对于第二行来说,由于上一行和这一行的至少两个格子的颜色是确定的,所以第二行每个格子的颜色都是确定的;后面的行也是同理
- 所以涂色的方案数是 $1$
考虑按照区间最小值进行分治,按照 $[1,n]$ 的最小值的出现位置把区间割开,对每个子区间分治下去,求出每个区间内:红蓝交错/不红蓝交错地填到区间最小值-1的高度的方案数,记为 $f_{l,r,0/1}$ 。
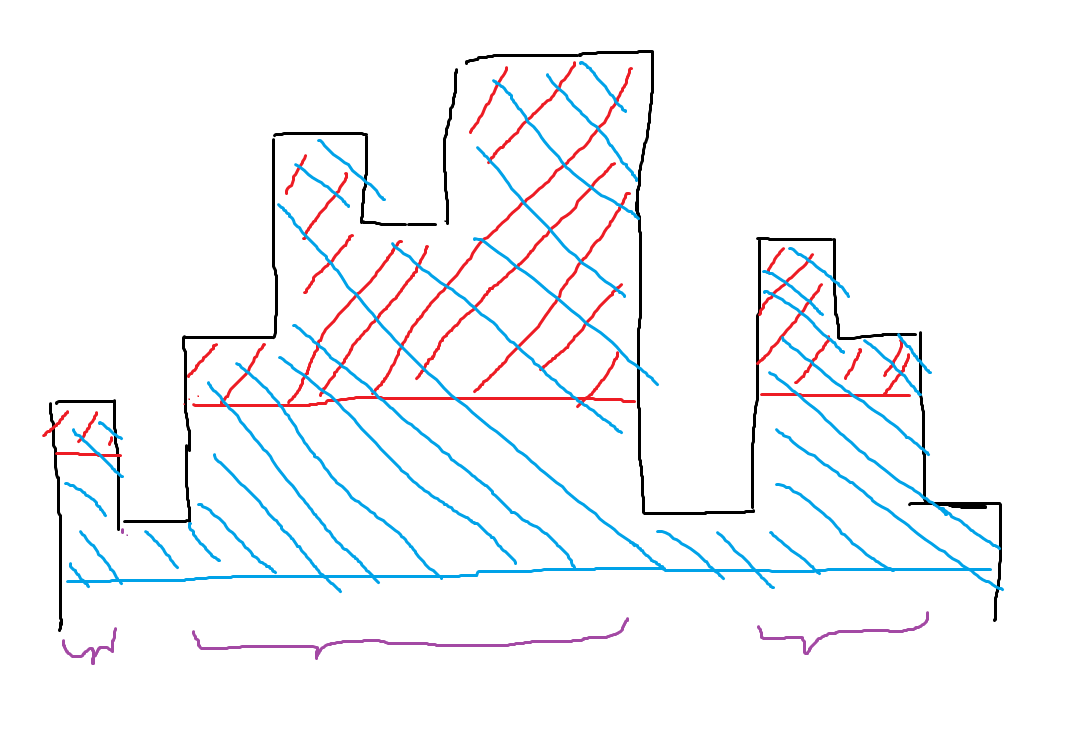
图中紫色的框出的是每一个子区间,红色标出每个子区间的 $f_{l,r,0/1}$ 考虑过的格子,蓝色标出大区间的 $f_{l,r,0/1}$ 需要考虑的格子。
合并子区间的信息,得到大区间的 $f_{l,r,0/1}$ 。直接算 $f_{l,r,1}$ 比较困难,可以考虑算总方案数,然后用总方案数减去 $f_{l,r,0}$ 。具体细节参见代码。