一个排列 $P$ 的冒泡排序交换次数达到下界当且仅当:对于某个位置 $i$ ,在它左边的、比 $P_i$ 大的数的个数不能超过 $\max\{0, i-P_i\}$ 个。
这个条件也等价于:
- 对于 $P_i\le i$ 的元素,它的右侧至少有 $(n-P_i) - (i-P_i) = n-i$ 个比它大的元素,也就是说它是后缀最小值
- 对于 $P_i \ge i$ 的元素,它是前缀最大值
此外一个观察是,对于任意的一个排列,除了 $P_i=i$ 的元素之外,不会有元素既是前缀最大值又是后缀最小值(因为既是前缀最大值又是后缀最小值也就意味着左边有 $P_i-1$ 个比它小的且右边有 $n-P_i$ 个比它大的)。
对于一个冒泡排序交换次数达到下界的排列 $P$ ,考虑把它的所有的前缀最大值都抠掉之后的序列:
- 这些剩下的元素不是前缀最大值,所以它们一定满足 $P_i < i$ ,也就是意味着它们一定是后缀最小值
- 所以,不是前缀最大值的元素一定是升序排列的
- 这也就意味着,只要知道了前缀最大值,就能够唯一地确定一个可能合法的排列 $P$
- 所以只需要对合法的前缀最大值序列计数就可以了
一个前缀最大值序列 $\{ M_i = \max_{j\le i} \{P_j\} \}$ 合法当且仅当 $M_{i-1}\le M_i \wedge M_i\ge i$ :
- 必要性:因为除了 $P_i = i$ 的元素之外不会有元素同时是前缀最大值和后缀最小值,故而是前缀最大值的元素一定都满足 $P_i \ge i$,所以必须有 $M_i \ge i$
- 充分性:
- 对于任意排列,是前缀最大值的元素都满足 $P_i \ge i$ ,满足 $P_i\ge i$ 必然是前缀最大值(左边的空位比小于它的数少)
- 将不是前缀最大值的位置升序填入之后,这些位置必然满足 $P_i < i$ (因为 $i$ 左边的空位置比小于 $i$ 的数少);$P_i < i$ 的位置必然是后缀最小值(大于它的数的数量超过了它右边的空位的数量)
故而只要统计满足 $M_i \ge i, M_{i-1} \le M_i$ 的 $\{M_i\}$ 的数量即可。
考虑折线模型。例如,对于排列 $\{2,3,1,5,4\}$ ,它前缀最大值序列对应到的折线是这样的:
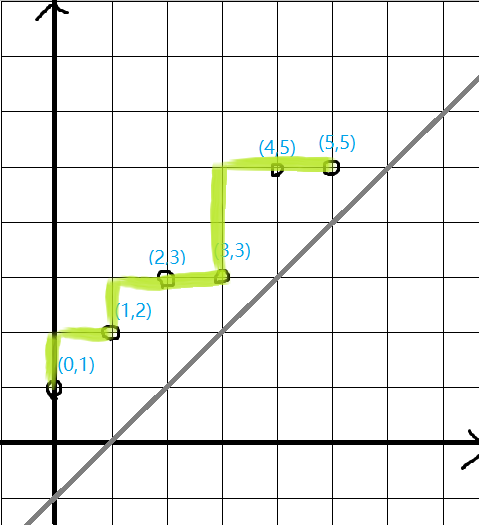
发现本质上就是一条从 $(0,1)$ 到 $(n,n)$ 且不经过直线 $y=x-1$ 的折线。
回到原题。设 $ans(x,y)$ 表示从 $(x,y)$ 出发走到 $(n,n)$ 不经过 $y=x-1$ 的方案数,也就是$\binom{2n-x-y}{n-x} - \binom{2n-x-y}{n+1-x}$。我们枚举排列 $p$ 与输入给出的 $q$ 第一个不同的位置 $i$ ,分以下几种情况讨论(设 $mx=\max_{j < i} \{ q_j \}$):
- $q$ 的长度为 $i-1$ 的前缀不合法:必然也不存在合法的 $p$ ,所以对答案的贡献是 $0$
- $q$ 的长度为 $i-1$ 的前缀合法:
- $q_i > mx$
- 由于要求 $p_i > q_i$ ,所以 $p_i$ 也必然是个前缀最大值,所以方案数是 $ans(i-1,q_i + 1)$
- $q_i < mx$
- $p_i > mx$ :此时方案数是 $ans(i-1,mx+1)$
- $p_i < mx$ :将不是前缀最大值的数依次升序填入不是前缀最大值的位置,如果到 $i$ 这个位置,该填的数大于 $q_i$ ,这种情况就对答案产生 $ans(i,mx)$ 的贡献;否则贡献为 $0$ 。
- $q_i > mx$
预处理阶乘及其逆元就可以在 $O(1)$ 的时间内统计 $i$ 的贡献。总时间复杂度 $O(n)$ 。