LOJ3090 「BJOI2019」勘破神机

my submission on loj.ac

$m=2$

设填满 $2\times n$ 的方案数为 $f_n$，则 $F(n,k) = \binom {f_n}{k}$，而 $\binom{f_n}{k}$ 可以展开为一个关于 $f_n$ 的 $k$ 次多项式。故而问题转化为了：对于每个 $j\in [0,k]$，求 $\sum_{n=l}^r f_n^j$ 。

显然 $f_n = f_{n-1}+f_{n-2}$（考虑最后一列填两个横着的还是填一个竖着的）。

该递推式的特征根为 $x_1 = \frac{1+\sqrt 5}{2}, x_2 = \frac{1-\sqrt 5}{2}$，由 $f_0=1,f_1=1$ 解得通项公式为 $f_n = \frac{5+\sqrt 5}{10}x_1^n +\frac{5-\sqrt 5}{10} x_2^n$。

令 $A=x_1,B=x_2,p=\frac{5+\sqrt 5}{10},q=\frac{5-\sqrt 5}{10}$，则 $f_n = pA^n + qB^n$。

而我们要求的是

$$\begin{aligned} &\sum_{n=l}^r f_n^j\\ =& \sum_{n=l}^r (pA^n + qB^n)^j\\ =& \sum_{n=l}^r \sum_{i=0}^j \binom{j}{i} (pA^n)^i (qB^n)^{j-i}\\ =& \sum_{i=0}^j \binom{j}{i} p^i q^{j-i} \sum_{n=l}^r (A^iB^{j-i})^n \end{aligned}$$

最后面是个等比数列求和，可以分治求解。

$m=3$

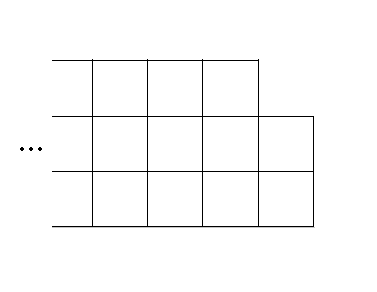
设填满一个 $3\times n$ 的网格的方案数是 $f_n$，填满一个 $3\times n + 2$ 的网格的方案数为 $g_n$。其中，$3\times n + 2$ 的网格定义如下：

枚举 $3\times n$ 的网格中最靠右的颗粒进行讨论，得到 $f_n = f_{n-2} + 2g_{n-2}$

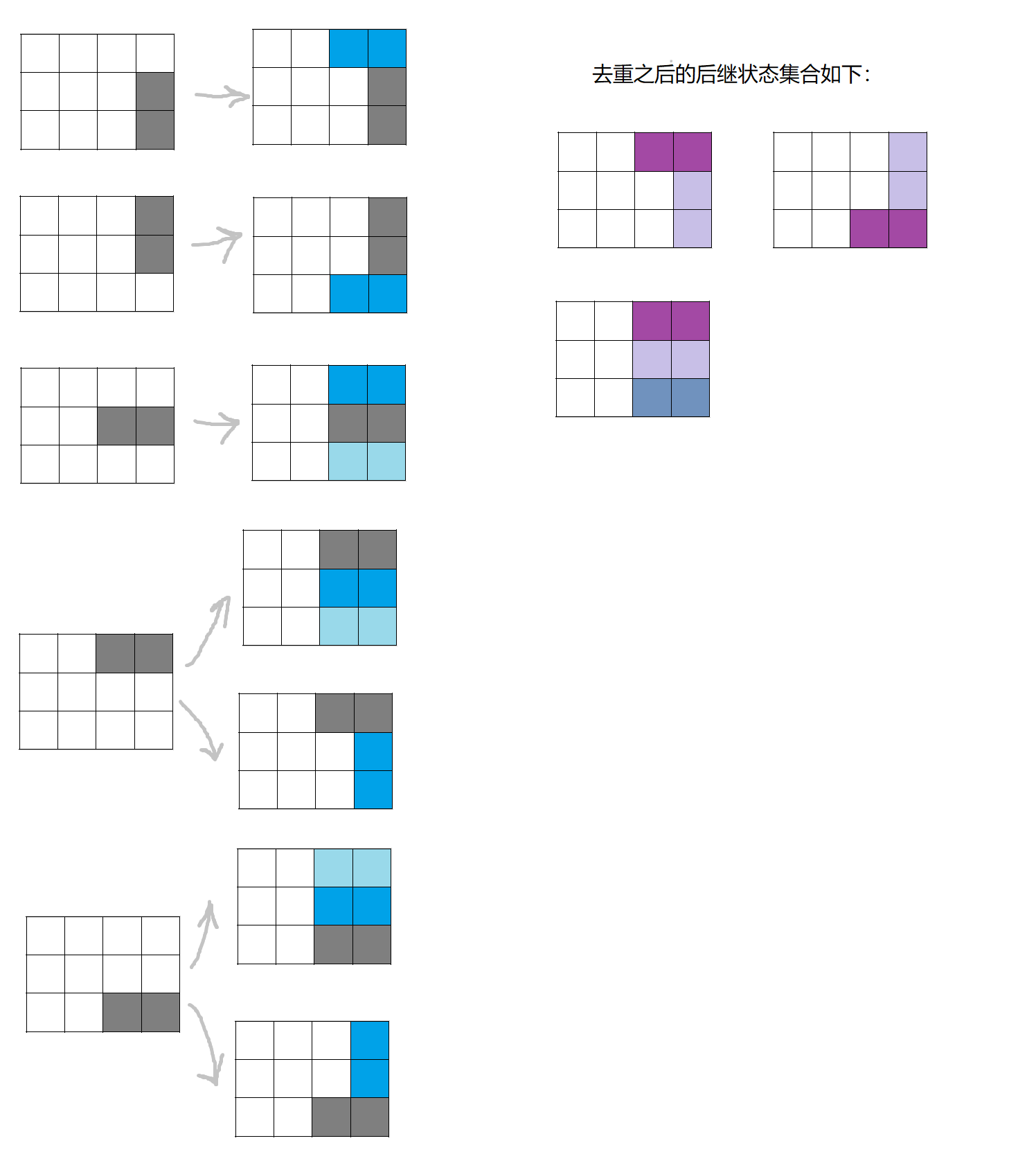
同理得到 $g_n = f_{n} + g_{n-2}$

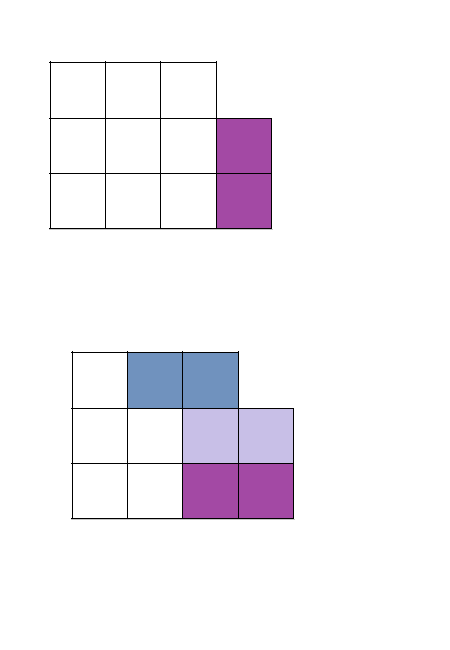
将 $g$ 的递推式展开得到 $g_n = f_n + f_{n-2} + f_{n-4} + \cdots + f_0$

对于任意的 $2\nmid n$ 显然有 $f_n = g_n = 0$。不妨设 $F_n = f_{2n}, l’=\lceil\frac{l}{2}\rceil, r’=\lfloor\frac{r}{2}\rfloor$。与 $m=2$ 的方法同理，我们只要求出 $\sum_{n=l’}^{r’} F_n^i$ 即可。

$$\begin{aligned} F_n & = 3F_{n-1} + 2\sum_{i=0}^{n-2} F_i\\ F_n - F_{n-1} & = (3F_{n-1} + 2F_{n-2}) - (3F_{n-2})\\ & = 3F_{n-1}-F_{n-2}\\ \therefore F_n &= 4F_{n-1}- F_{n-2} \end{aligned}$$

特征根为 $x_1 = 2+\sqrt 3, x_2 = 2-\sqrt 3$，带入 $F_0 = 1, F_1 = 3$ 得 $F_n = \frac{3+\sqrt 3}{6} x_1^n + \frac{3-\sqrt 3}{6} x_2^n$，和 $m=2$ 的情况类似做就可以了。