对于一个已经无法继续旋转的多边形,我们考虑它上面的一个四边形,其顶点依次为 $A,B,C,D$($O$ 点表示多边形的 $1$ 号顶点):
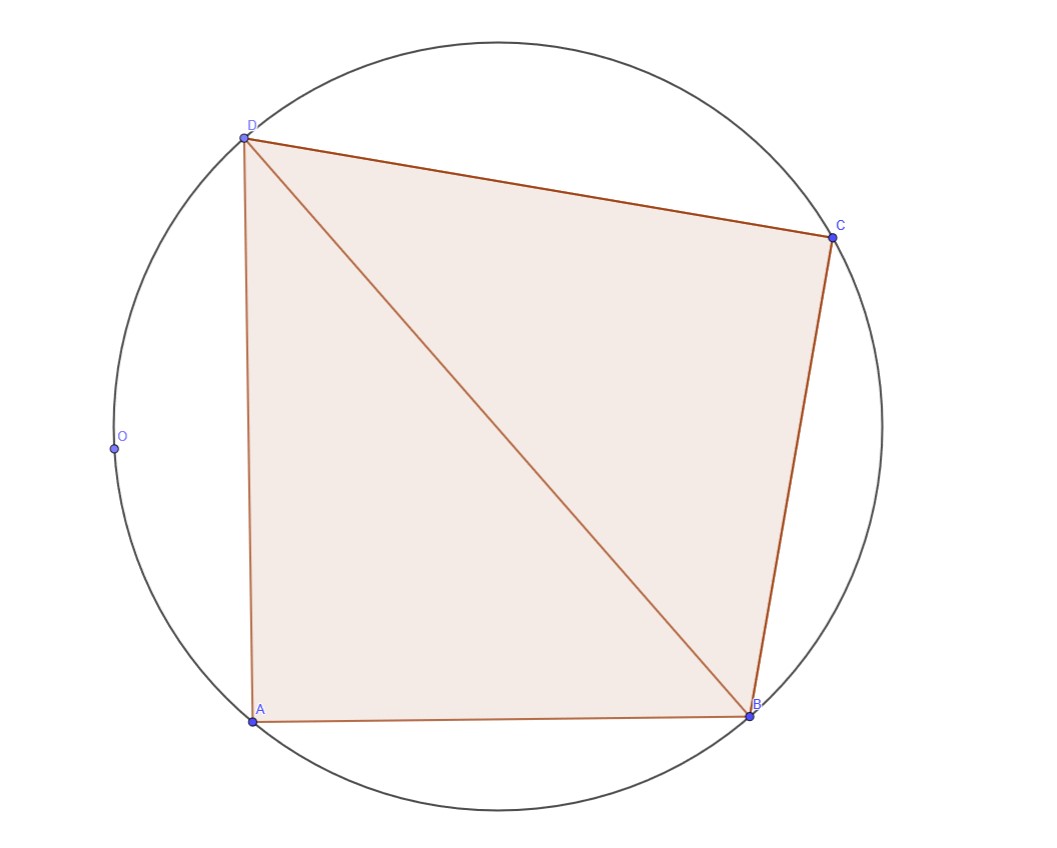
从 $C$ 到 $D$ 的这一段:
- 假设以 $CD$ 为一边的另一个三角形为 $\triangle CDT_1$(显然 $T_1\in (C,D)$,$CD$ 无法再旋转)
- 不可能有以 $T_1C$ 为一边的异于 $\triangle CDT_1$ 的三角形(否则 $CT_1$ 将可以旋转)
- 可以有以 $T_1D$ 为一边的异于 $\triangle CDT_1$ 的三角形,设为 $\triangle DT_1T_2$
- 不可能有以 $T_2T_1$ 为一边的异于 $\triangle DT_1T_2$ 的三角形,但是可以有以 $DT_1$ 为一边的异于 $\triangle DT_1T_2$ 的三角形,设为 $\triangle DT_2T_3$
- ……
从 $B$ 到 $D$ 这一段:不可能有以 $BC$ 为边且不同于 $\triangle BCD$ 的三角形,否则 $BC$ 将可以旋转。从 $A$ 到 $B$ 的这一段同理。
从 $D$ 到 $A$ 的这一段:
- 如果有以 $AD$ 为一边的异于 $\triangle ABD$ 的三角形,设为 $\triangle ADP_1$:
- $P_1\in (D,n]$,那么 $AD$ 就可以旋转了
- 如果 $P_1\in [1, A-1)$ 则是合法的
- 不可能有以 $P_1A$ 为一边异于 $\triangle AP_1D$ 的三角形,因为这样 $P_1A$ 就可以旋转了
- 可以有以 $P_1D$ 为一边的异于 $\triangle AP_1D$ 且另一顶点 $\in [1,P_1)$的三角形,设为 $\triangle DP_1P_2(P_2 \in [1,P_1))$
- 不可能有以 $P_1P_2$ 为一边的异于 $\triangle DP_1P_2$ 的三角形,但是可以有以 $DP_2$ 为一边的异于 $\triangle DP_1P_2$ 且另一顶点位于 $[1,P_2)$ 的三角形,设为 $\triangle DP_2P_3$
- ……
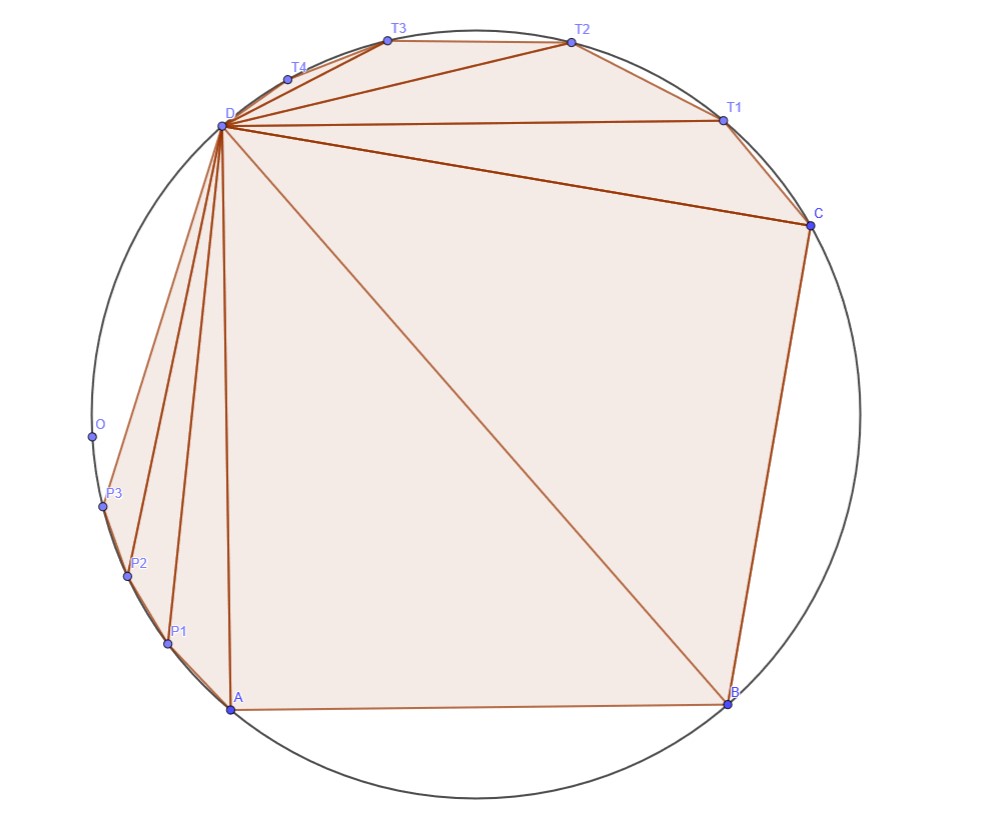
综上所述,一个多边形如果无法继续旋转,那么除了 $n$ 号点以外的每个点必须直接和 $n$ 号点相连。
对于一个状态,发现它不直接连接 $n$ 和其它点的边会形成一个树形结构(实际上是个二叉树森林):
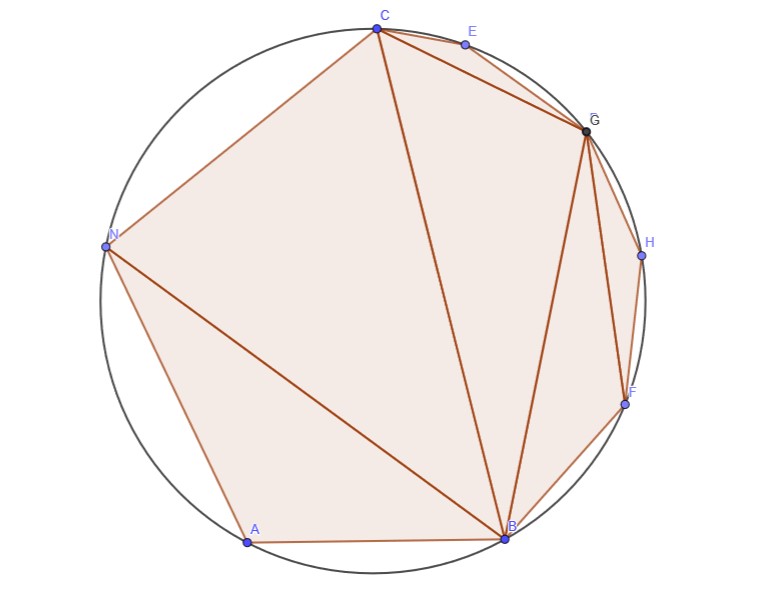
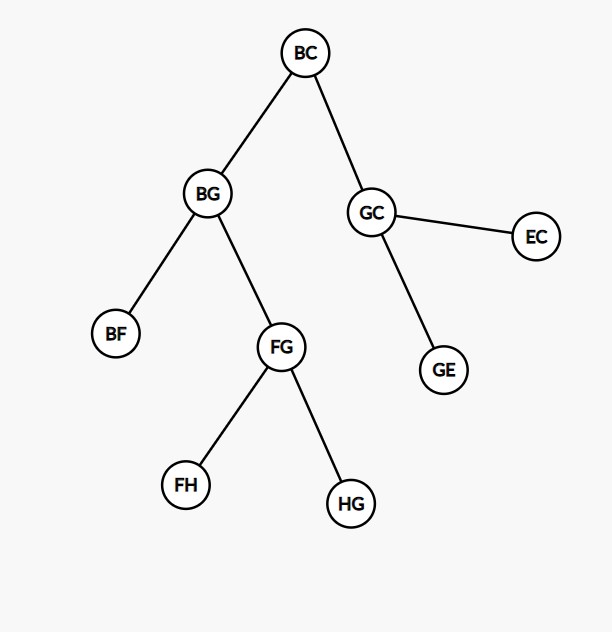
最小的操作次数就是树上的点数(即多边形中不直接连接 $n$ 和其它点的边数);操作的方案数也就是将树中的点排列使得祖先总是在自己之前出现的方案数。一个经典结论是这样的排列方案数为点数的阶乘除以每个点的子树大小。
考虑在初始状态上进行一次旋转会造成什么样的影响:
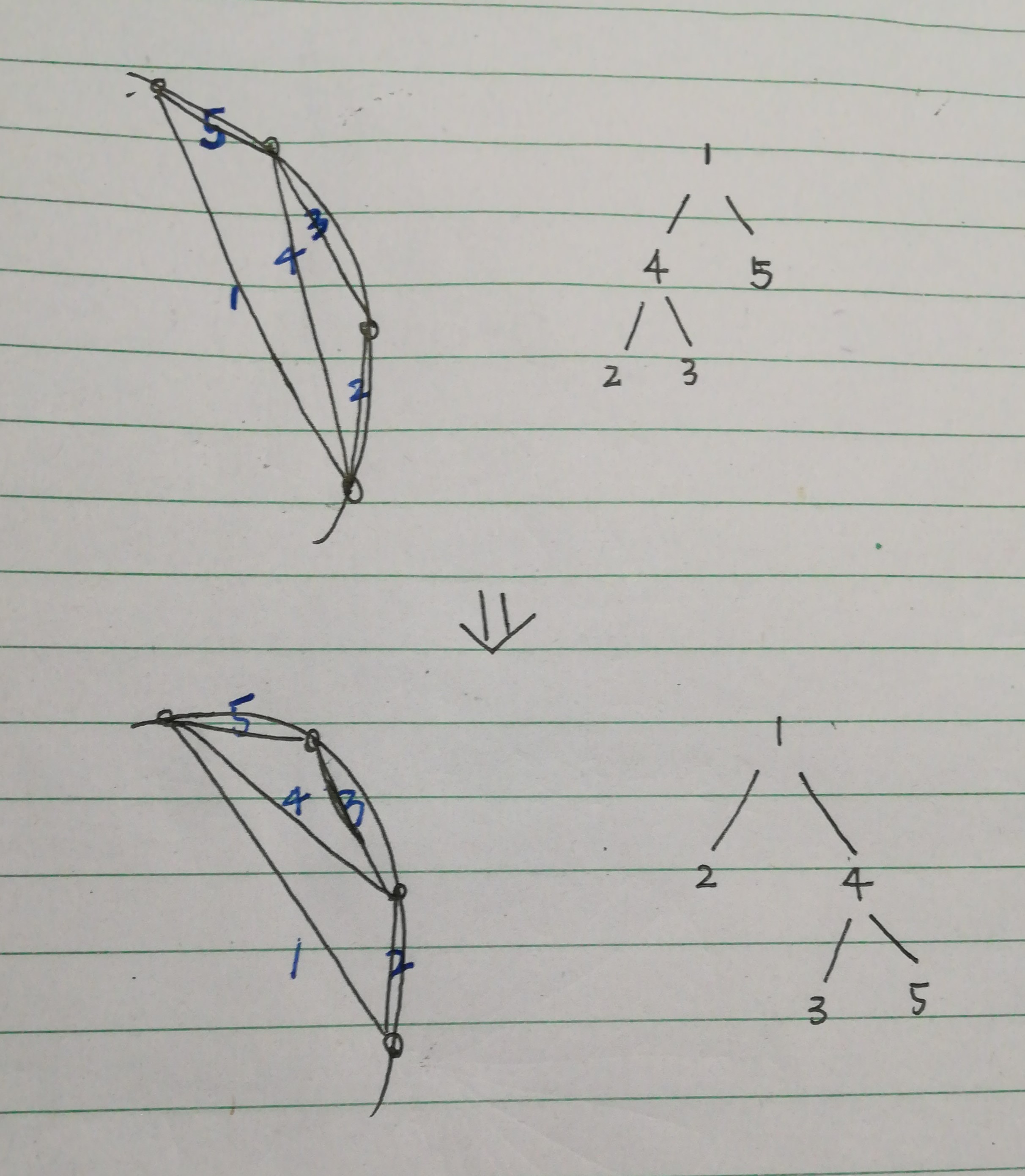
发现只有被旋转的那条边的子树大小改变了。预处理出初始状态的操作方案数,就能快速地得到旋转之后的答案。注意特判被旋转的边为根的情况。