坐标轴的旋转变换

将$(x_1,y_1)$和$(x_2,y_2)$分别作为$ x$轴和$ y$轴（即将坐标轴旋转，使得$x$轴与$(x_1,y_1)$平行，$y$轴与$(x_2,y_2)$平行，也就是将$(x_1,y_1)$，$(x_2,y_2)$作为单位向量），需要求出其他的点在旋转后的坐标系里的坐标。

如何实现？考虑原来的向量$(x,y)$表示的向量实际上是$xi+yj$，也就是单位向量$i$的$x$倍 + 单位向量$j$的$y$倍。因此，可以设这个点变化后的坐标为$(x’,y’)$，则：

$$\begin{cases} x=x'\cdot x_1 + y' \cdot x_2\\ y=x'\cdot y_1 + y' \cdot y_2\\ \end {cases}$$

解得

$$\begin{cases} x'={xy_2-x_2y\over x_1y_2-x_2y_1}\\ y'={x_1y-xy_1\over x_1y_2-x_2y_1} \end{cases}$$

看起来就是叉乘的乘积——可是为什么呢？

让我们来看一幅图：

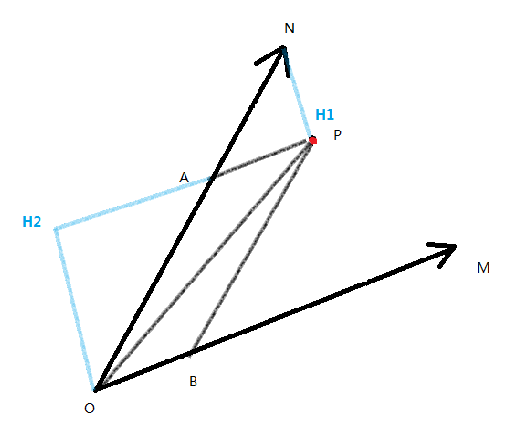
设$P(x,y)$为我们要计算的点，$OM,ON$分别为两个“单位向量”，过$P$作单位向量的平行线$PA//OM,PB//ON$，则$x’={OB\over OM},y’={OA\over ON}$。

现在要证明的就是：

$$\begin{cases} {S_{\triangle OPN}\over S_{\triangle MON}}={OB\over OM}\\ {S_{\triangle OPM}\over S_{\triangle MON}}={OA\over ON}\\ \end{cases}$$

第一个式子等价于${S_{\triangle OPN}\over AP}={S_{\triangle MON}\over OM}$。

过$N,O$分别作$AP$的垂线交AP于$H_1,H_2$，则$S_{\triangle OPN}={1\over 2} AP \cdot (OH_2+NH_1)$，$S_{\triangle MON} ={1\over 2}OM\cdot (OH_2+NH_1)$，上式得证。同理可以证明第二个式子。