定理:三角形的垂心(orthocenter)、重心(centroid)、外心(circumcenter)共线,且重心到垂心的距离等于重心到外心的距离的两倍。过三角形的垂心、重心、外心的直线称为欧拉线(Euler line)。
可以在这里感受一下。
证明:
令$\triangle_{ABC}$的垂心,重心,外心分别为$O_1,O_2,O_3$
分别作$AB,BC,CA$的中点$E,F,D$,则$EF,ED,FD$是$\triangle_{ABC}$的中位线,$\triangle_{ABC}\sim \triangle_{FDE}$且相似比为$2:1$。
由重心的性质得$BD$过$O_2$且$\frac{BO_2}{DO_2} = 2$。
由垂心的定义得$O_1B\perp AC$。
由于外心是边的垂直平分线的交点,且$D$是$AC$的中点,所以$O_3D\perp AC$。所以有$O_1B \parallel O_2D$。
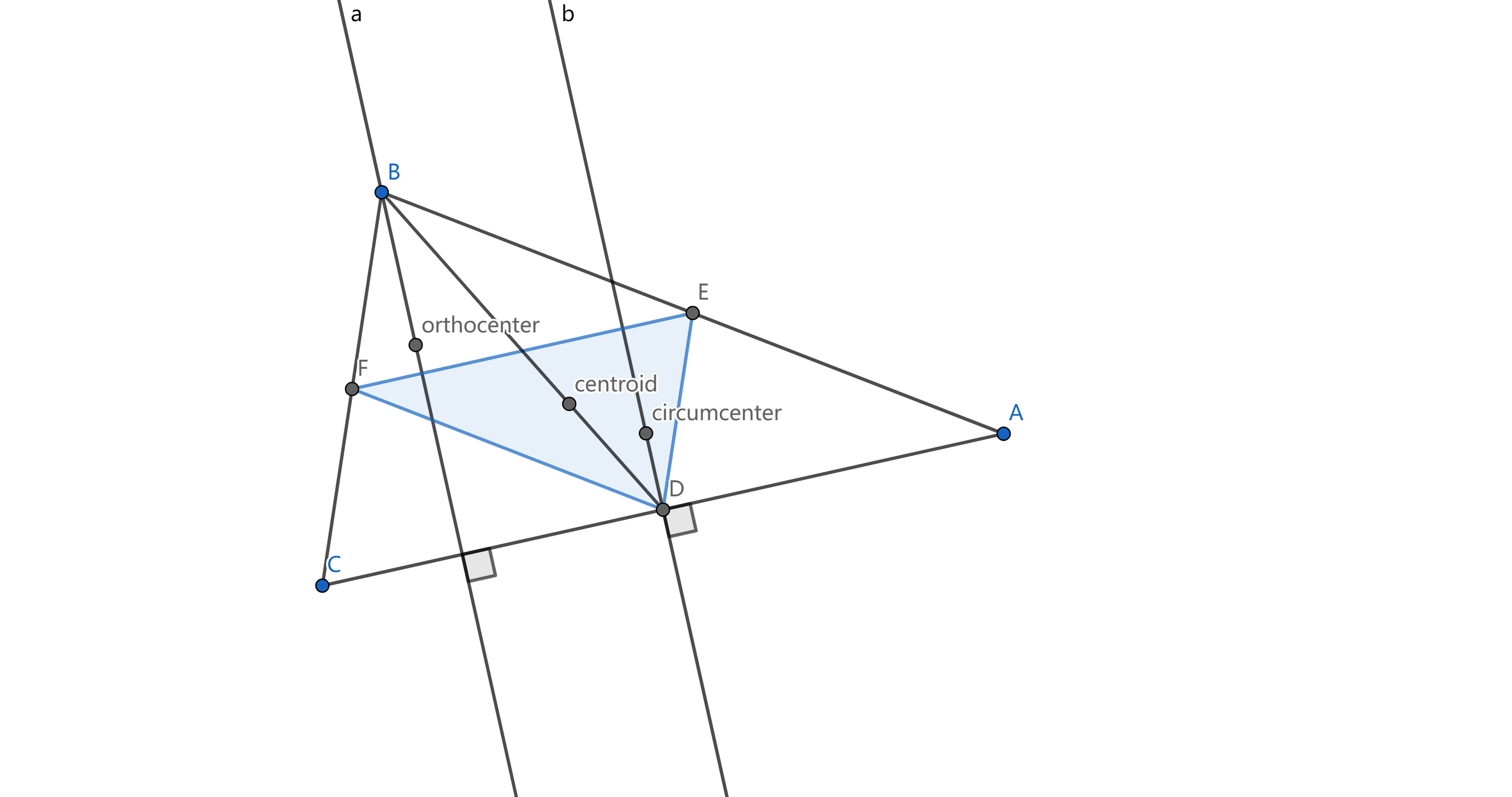
由于$EF\parallel AC, O_3D\perp AC$,所以$O_3D\perp EF$。同理可以证明,$O_3F\perp ED,O_3E\perp FD$。所以$\triangle_{ABC}$的外心和$\triangle_{DEF}$的垂心重合。
由$\triangle_{ABC}\sim \triangle_{FDE}$知$B$到$\triangle_{ABC}$的垂心的距离等于$D$到$\triangle_{DEF}$的垂心的距离的两倍,也就是说$2DO_3=BO_1$。又因为$2DO_2 = BO_2,\angle O_1BO_2 = \angle O_2DO_3$,所以$\triangle_{BO_2O_1}\sim \triangle_{DO_2O_3}$。
由$\triangle_{BO_2O_1}\sim \triangle_{DO_2O_3}$知$\frac{O_1O_2}{O_2O_3} = \frac{BO_2}{DO_2} = 2$,$\angle BO_2O_1 = \angle DO_2O_3$。又因为$B,O_2,D$共线,所以$O_1,O_2,O_3$共线。
证毕。