五边形数定理

参考

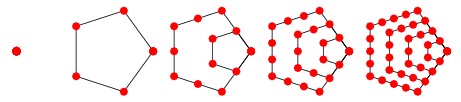
如图，定义五边形数的第$i$项为第$i$张图中的点数，$f_i = f_{i-1} + 3(i-1)+1 = {n(3n-1)\over 2}$。

对于i=1,-1,2,-2,……定义广义五边形数，取值依次为：1 2 5 7 12 15 22 26 35 40 51 57 70 77 92 100 117 126 145 155 176 187 210 222 247……

定义欧拉函数为：

$\phi (x) = \prod_{i=1}^{\infty} (1-x^i)$

$\phi(x) = \sum_{i=-\infty}^{\infty } (-1)^i x^{i(3i-1)\over 2} \\ = 1 + \sum_{i=1}^{\infty}(-1)^i(x^{i(3i-1)\over 2} + x^{i(3i+1)\over 2})$

设$P_i$表示$i$的整数划分数，考虑它的生成函数$F(x)$：

$F(x)= \prod_{i=1}^{\infty } (1+x^i + x^{2i} + x^{3i} + \cdots ) \\ =\prod_{i=1}^{\infty } {1\over 1-x^i} \\ ={1\over \phi (x)}$

求出$\phi (x) $之后，多项式求逆即可。

如果没有取模的话，也可以把$F(x) \phi(x) = 1$暴力展开得到一个递推式，由于$\phi(x)$只有$\sqrt n$项有值，所以直接递推是$O(n\sqrt n)$的。