Sol

参考了zzq的blog

考虑分块。对于一次询问，涉及到的元素有如下的形式：

Sol

设 $s(l_1,r_1,l_2,r_2) = \sum_{i\in [l_1,r_1]} \sum_{j\in [l_2,r_2]} [i < j \wedge a_i > a_j]$ 。

考虑莫队算法，当右端点从$r-1$移动到$r$的时候，答案的改变量是

首先添加试题，然后选择“添加多组测试点”。

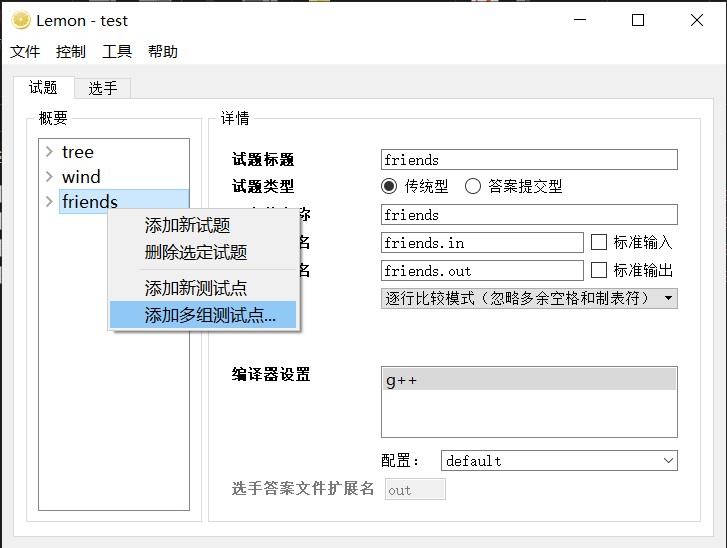
在出现的测试点添加向导中，可以直接点击下一步。每个测试点（也就是每个子任务）的时间、空间限制以及分值都是可以在配置完成之后单独调整的。

Sol

容易想到$O(Bell(P))$地枚举$P$的集合划分，然后进行容斥（强制同一个集合里的数取值相同），但是容斥系数应该如何取呢？

对于一个大小为$x$的集合，设它的容斥系数为$f_x$。一种集合划分的容斥系数为每个集合的容斥系数的乘积。

Sol

2016年集训队论文的第二篇讲到了这道题，但是论文中的建图方式似乎会出现负环（也有可能是我写炸了？）。下面的建图方法是从KIDGIN7439的这篇博客中看到的，因为觉得原文的阐述十分不清楚，重新阐述如下。

首先枚举$lim$为每一行、每一列的部件数量的最大值。求出在$lim$限制下能个放的最大零件数$tot’$，只要判断$lim \le \lfloor tot’ \cdot \frac{A}{B} \rfloor$是否成立，就能限制为$lim$时是否存在合法的方案，并更新答案。

day 1

A - 排列

题意

day1

A - 递增树列

题意

Sol

这道题的建图方法：

1. 每个筐拆成三个点分别代表三个位置，三个点两两之间互相连边
2. 每个球向它可以放入的筐的三个点都连边

推荐两个带花树算法的学习资料：维基百科 Bill Yang’s blog

Q1

缩掉奇环之后，会不会存在一条交错路，和奇环相交的部分没有经过花根，成为了一条在缩掉了花之后的图中找不到的增广路？

Sol

考虑多项式乘法的组合意义，枚举第$i$项被选的次数$b_i$，要求$\sum b_i = m, \sum b_i i = k$，则对应的贡献为

如果$p \mid m$，我们对上面的式子应用Lucas定理，发现：