问题：给出两个多项式，以及模数$P$，计算它们的卷积，不保证$P$是$t\cdot 2^k + 1$的形式的质数。
模数不支持NTT，那么我们肯定只能通过某种方式算出精确值，然后再取模。然而，两个这样的多项式相乘，每一项的系数最大是$n\cdot P^2$，大约$10^{23}$，FFT会爆精度，也不可能单模数NTT……
对数组长度有要求的FFT
CTSC2010 循环卷积
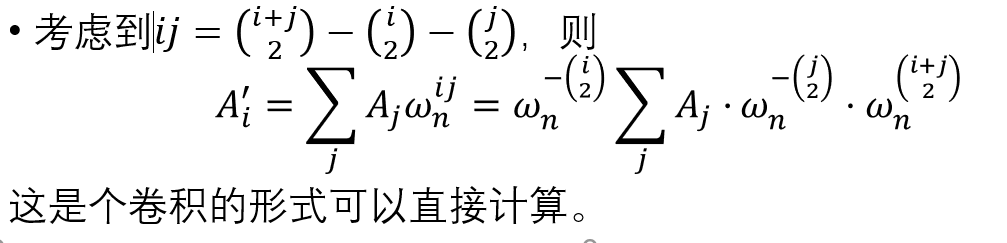
有两个长度为$n$的多项式$A$和$B$，需要求出$AB^C$。其中的$$运算定义如下：
数据范围：$n\le 5\times 10^5,C\le 10^9$。保证$n$一定可以被分解成若干个不超过$10$的正整数的乘积，并且$n+1$是质数。
公平组合游戏的经典模型
Sprague–Grundy theorem(SG定理)
Nim积
Nim游戏 结论及证明
设初始状态中，每一堆的石子个数分别$\{a_1,a_2,a_3\cdots a_n\}$。则先手获胜的充要条件是$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n \neq 0$。
证明：
- 终止状态满足$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n=0$。
- 每一个$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n=0$的状态，都只能够转移到$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n\neq 0$的状态。因为假设操作后$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n$仍然是$0$，则有$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_i\bigoplus \cdots a_n = a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_i ‘\bigoplus \cdots a_n$，则$a_i = a_i’$，推出矛盾。
- 每一个$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n\neq 0$的状态，都可以转移到$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n=0$的状态。因为假设$a_1\bigoplus a_2\bigoplus a_3\bigoplus\cdots a_n=k$，，设$k$二进制下最高的为$1$的位是$p$，那么$a_1,a_2\cdots a_n$中一定存在一个数$a_i$满足$a_i$的第$p$位是$1$，从而我们可以推出$a_i \bigoplus k < a_i$（高于第$p$位的不变，第$p$位从$1$变成了$0$），将$a_i$改成$a_i \bigoplus k$即可。