my submission on loj.ac

不难发现问题等价于：把每棵树划分成若干条链，把这些链拿来做圆排列，要求相邻的链不能来自同一棵树，求方案数。

假设我们已经把每棵树划分成了若干条链，并且确定好了链在圆排列中出现的方向（长度大于 $1$ 的链有两种可能的方向），求圆排列方案数。假设此时第 $i$ 棵树的点划分成了 $A_i$ 条链。

参考资料

• IOI2018 集训队论文 高睿泉 《浅谈保序回归问题》
• 大米饼的博客

Sol

my submission on loj.ac

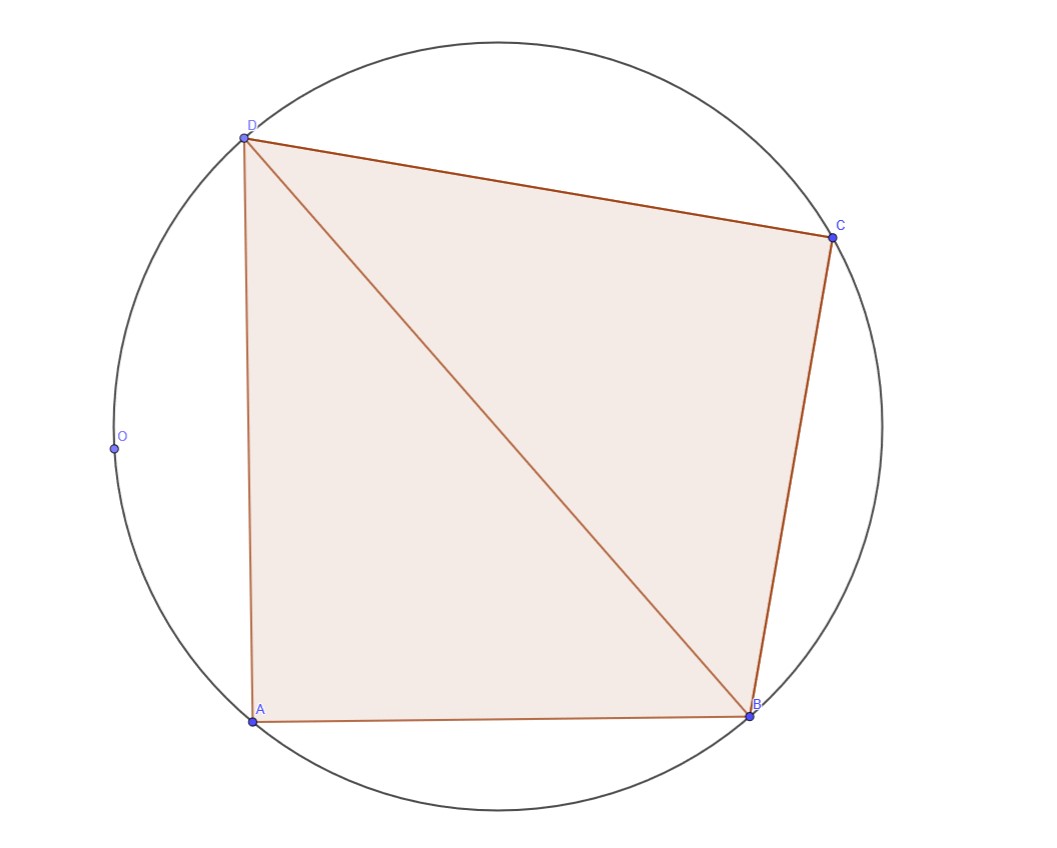
对于一个已经无法继续旋转的多边形，我们考虑它上面的一个四边形，其顶点依次为 $A,B,C,D$（$O$ 点表示多边形的 $1$ 号顶点）：

A - 同桌与室友

相当于是有一张图，边有两种，与每个点相邻的每种边至多有一条。求有多少种重标号的方案，使得重标号前后的图相同。

由于每个点的度数不超过 2，我们可以对连通块的形态讨论（每个连通块要么是链，要么是环）。

参考资料

• OI-wiki(没有证明)
• 通过 google search 找到的一篇资料

引理

my AC submission

关于题意的补充说明

• 令 $\alpha(0\le \alpha < 2\pi)$ 为 $\overrightarrow{DA}$ 逆时针旋转到 $\overrightarrow{DE}$ 经过的角度，$\beta ( 0\le \beta < 2\pi )$ 为 $\overrightarrow{DA}$ 逆时针旋转到 $\overrightarrow{DF}$ 经过的角度，那么题意中对 $\angle ADE, \angle ADF$ 的限制等价于：$\frac{1}{2} \pi < \alpha, \beta < \frac{3}{2} \pi$。
• 可以参考我的这份O(n^6)暴力来确认自己没有读错题意。

• my submission on loj.ac
• 参考了 zsy的博客

设

那么（可以类比奇自然数和偶自然数的 EGF）

• my AC submission on loj.ac
• my O((R-L)n) solution on loj.ac
• 参考了memset0的博客和fcwww的博客

设 $W$ 为初始根节点的权值。由于每个叶子的权值互不相同，所以 $W$ 来自的叶子结点唯一。

改变 $W$ 的策略有以下三种：

my submission on loj.ac

设 $f_i$ 表示从第 $i-1$ 块玻璃和第 $i$ 块玻璃之间向第 $n$ 块玻璃的方向射出了一束大小为 $1$ 的光线，最终能穿过第 $n$ 层玻璃的光的数量。特别地，$f_{n+1} = 1$，你可以想象成在第 $n$ 块玻璃的后面还有一块反射率为 $0\%$、透光率为 $100\%$ 的玻璃。

下文中的 $a_i,b_i$ 为原题中的 $a_i\%, b_i\%$。

my submission on loj.ac

$m=2$

设填满 $2\times n$ 的方案数为 $f_n$，则 $F(n,k) = \binom {f_n}{k}$，而 $\binom{f_n}{k}$ 可以展开为一个关于 $f_n$ 的 $k$ 次多项式。故而问题转化为了：对于每个 $j\in [0,k]$，求 $\sum_{n=l}^r f_n^j$ 。