组合计数练习题

UOJ422 小z的礼物

考虑min-max容斥：

$$\max (S) = \sum_{T\subseteq S} (-1)^{|T|+1} \min (T)$$

对希望得到的物品的每一个子集，求出期望最早什么时候子集里至少有一个物品被拿到了，就能算出答案。

设包含了至少一个这个子集内的物品的相邻的格子对的数量是$a$，所有的相邻的格子对的数量是$b$，那么这个期望值就是$b\over a$。$a$是一个定值；$b$则可以看做（子集内每一个物品包含它的相邻格子对数量的和）-（同时包含了子集内的两个物品的相邻格子对的数量）。

设$f_{S,t}$表示上一列选了的格子的集合是$S$，之前选过的格子的（子集内每一个物品包含它的相邻格子对数量的和）-（同时包含了子集内的两个物品的相邻格子对的数量）为$t$，所有方案的容斥系数的和。用类似轮廓线dp的方法转移，就可以做到$O(2^n n^2m^2)$的复杂度。

Code

LOJ2320「清华集训 2017」生成树计数

把原题的式子换一个表达的方式：把每个连通块看做一个点，设$d_i$为每个点的度数，则

$$val (T) = (\sum_{i=1}^n d_i^m) (\prod_{i=1}^n d_i^m )(\prod_{i=1}^n a_i^{d_i})$$

因为式子里面有度数，所以考虑用prufer序列来计数。枚举每一个点在prufer序列中出现的次数$k_i$，得到

$$Ans = \sum_{k_1+k_2+\cdots +k_n=n-2} {(n-2)!\over k_1!k_2!\cdots k_n!} \cdot \sum_{i=1}^n (k_i+1)^{2m}a_i^{k_i+1} \prod_{j\neq i} (k_j+1)^ma_j^{k_j+1}$$

设

$$\begin{aligned} A_i(x) = \sum_{k=0}^\infty {a_i^{k+1}(k+1)^m\over k!} x^k\\ B_i(x) = \sum_{k=0}^\infty {a_i^{k+1}(k+1)^{2m} \over k!}x^k \end{aligned}$$

则

$$Ans= (n-2)!\sum_{i=1}^n (B_i(x)\prod_{j\neq i} A_j(x) )[x^{n-2}]$$

因为$A_i(x)$里面有指数为$k+1$，还有$x^k \over k!$，所以尝试对$A_i(x)$积分得到$T(x)$：

$$\begin{aligned} T(x) = \sum_{k=0}^\infty {a_i^{k+1}(k+1)^m \over (k+1)!} x^{k+1}\\ =\sum_{k=1}^\infty {a_i^kk^m\over k!}x^k \end{aligned}$$

将$k^m$展开：

$$\begin{aligned} T(x) = \sum_{k=1}^\infty {a_i^k \over k!} x^k \sum_{j=0}^{\min\{m,k\}} \begin{Bmatrix}m\\ j\end{Bmatrix} {k\choose j} j! \end{aligned}$$

把${k\choose j}j!$与前面的$k!$抵消，得到

$$\begin{aligned} T(x) = \sum_{k=1}^\infty a_i^k x^k \sum_{j=0}^{\min\{m,k\}} {1\over (k-j)!}\begin{Bmatrix}m\\ j\end{Bmatrix} \end{aligned}$$

把$j$提前

$$\begin{aligned} T(x) = \sum_{j=0}^m \begin{Bmatrix}m\\ j\end{Bmatrix} \sum_{k=j}^\infty {a_ix^k\over (k-j)!}\\ =\sum_{j=0}^m \begin{Bmatrix}m\\ j\end{Bmatrix} a_i^jx^j \sum_{k=0}^\infty {a_i^kx^k\over k!}\\ =\sum_{j=0}^m \begin{Bmatrix}m\\ j\end{Bmatrix} a_i^jx^j e^{a_ix} \end{aligned}$$

然后对$T(x)$求导得到$A_i(x)$

$$\begin{aligned} A_i(x) = T'(x)\\ =\sum_{j=0}^m \begin{Bmatrix}m\\ j\end{Bmatrix} (j \cdot a_i^jx^{j-1} e^{a_ix} + a_i \cdot a_i^jx^j e^{a_ix}) \\ =\sum_{j=0}^{m} \begin{Bmatrix}m\\ j+1\end{Bmatrix} (j+1)( a_i^{j+1}x^je^{a_ix}) + \sum_{j=0}^{m} \begin{Bmatrix}m\\ j\end{Bmatrix} (a_i^{j+1} x^j e^{a_ix}) \\ = \sum_{j=0}^{m}(\begin{Bmatrix}m\\ j+1\end{Bmatrix} (j+1)+\begin{Bmatrix}m\\ j\end{Bmatrix} ) a_i^{j+1}x^je^{a_ix}\\ = e^{a_ix}\sum_{j=0}^{m}\begin{Bmatrix}m+1\\ j+1\end{Bmatrix} a_i^{j+1}x^j\\ \end{aligned}$$

对$B_i(x)$同理，得到

$$\begin{aligned} B_i(x) = e^{a_ix}\sum_{j=0}^{2m}\begin{Bmatrix}2m+1\\ j+1\end{Bmatrix} a_i^{j+1}x^j\\ \end{aligned}$$

所以

$$\begin{aligned} \sum_{i=1}^n B_i(x)\prod_{j\neq i} A_i(x)\\ = e^s \sum_{i=1}^n (\sum_{j=0}^{2m}\begin{Bmatrix}2m+1\\ j+1\end{Bmatrix} a_i^{j+1}x^j) \prod_{k\neq i}(\sum_{j=0}^{m}\begin{Bmatrix}m+1\\ j+1\end{Bmatrix} a_k^{j+1}x^j)\\ \end{aligned}$$

上式可以分治NTT求出。

Code

ARC062D Painting Graphs with AtCoDeer

每一个边双连通分量显然是独立的。所有边双的本质不同的染色方案数的乘积即是答案。

如果一个边双只包含一条边，那么答案显然是$K$。

如果一个边双恰好只有一个简单环，则是一个经典的Polya（有$K$种颜色的珠子，问有多少种旋转置换下本质不同的项链）。

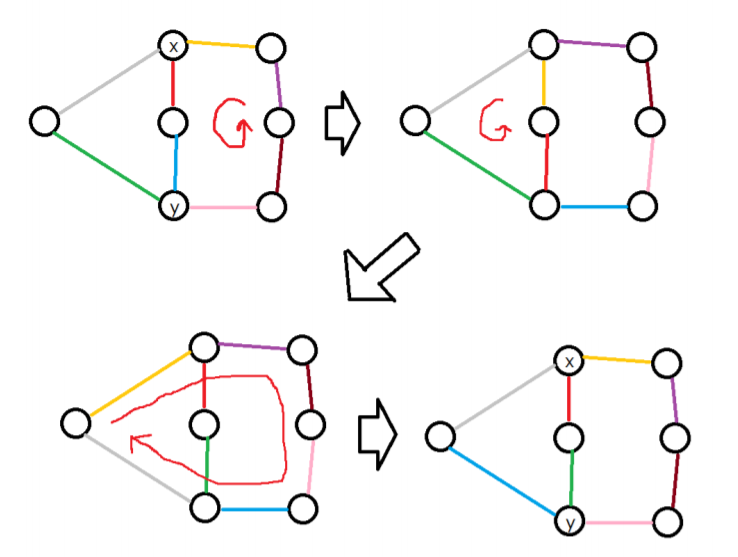
而如果一个边双包含多于一个环，则从下面的图（来自官方题解）可以看出，通过若干次操作我们可以交换一对相邻的边（下图中交换了绿色和蓝色的边）。故而两个给这个边双染色的方案是本质不同的，当且仅当它们染成某种颜色的边的数量不同。所以方案数为${K+C-1\choose K-1}$，其中$C$为这个边双内的边数。

Code

HDU6402 Boolean 3-Array

可以参考PE626，它是这道题的低维情形。

下文中的$A,B,C$表示原题中每一维的大小。

考虑简化题目中的置换：令$p_a,p_b,p_c$为三个长度分别为$A,B,C$的排列，每个排列的第$i$个元素表示这个维度上的swap操作使得最初的第$i$层到了哪个位置，令$a_i,b_i,c_i$分别表示每一维的第$i$层进行的翻转操作次数的奇偶性。我们规定先进行$p_a,p_b,p_c$的操作，再进行$a,b,c$的操作。那么原题中的一系列操作的结果将唯一对应到一组$(p_a,p_b,p_c,a,b,c)$。

利用Burnside lemma，数每一个置换的不动点数目。

先只考虑swap操作。枚举$p_a,p_b,p_c$的循环节，假设当前枚举到的循环节长度分别为$la,lb,lc$，考虑循环节中的方块对应的那个$la\times lb\times lc$的正方体。将每个点$(x,y,z)$与$({p_a}_x,{p_b}_y,{p_c}_z)$连边，则这些方块恰好会分裂成$la\cdot lb\cdot lc\over \operatorname{lcm}\{la,lb,lc\}$个连通块（并且每个连通块都是一个环）。显然每个连通块内的格子必须填同一个数，不同连通块的格子没有影响。

考虑flip操作对每一个连通块的影响：记$d_{x,y,z} = (a_x+b_y+c_z) \bmod 2$，则如果连通块内所有点的$\sum d_{x,y,z}$为奇数，则不存在不动点；否则，如下图，环上打了叉的点表示$d_{x,y,z}=1$的点，箭头表示置换的方向：

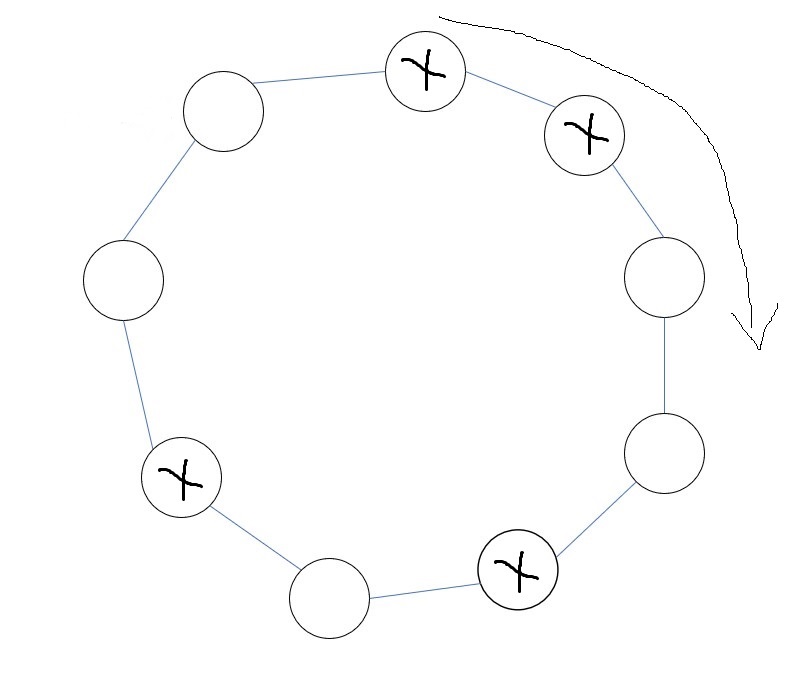
那么显然只有两种填数方案是不动点：

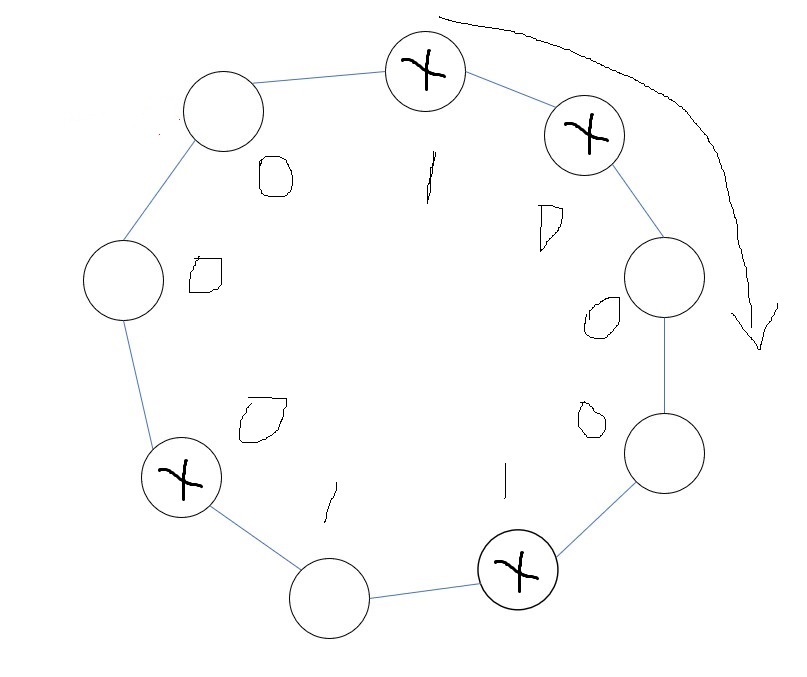
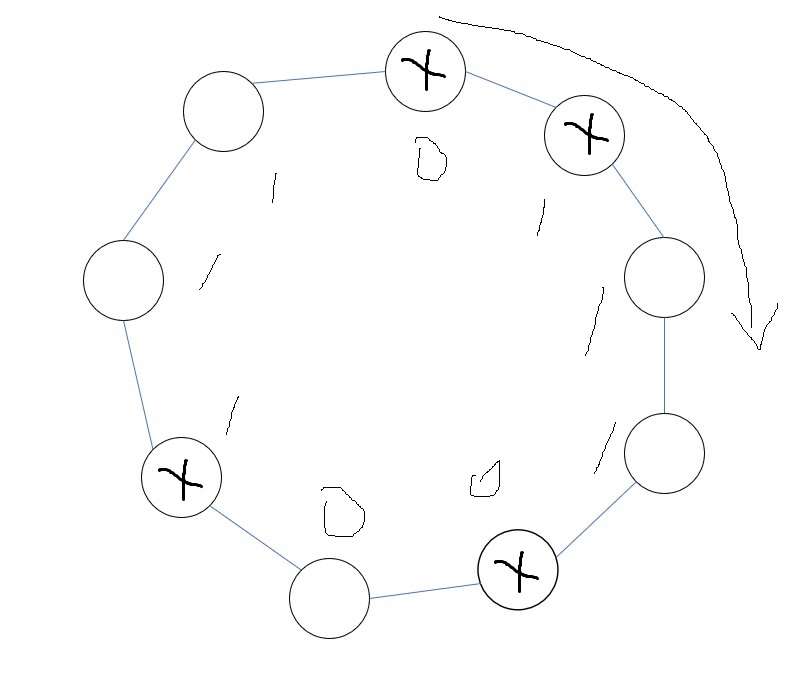
首先枚举$p_a,p_b,p_c$的每种长度的循环节的出现次数（设$k_i,l_i$表示长度为$l_i$的循环节出现了$k_i$次，那么对应的排列数是$n!\over \prod l_i^{k_i} k_i!$），然后求出对于每一组循环节的每一个连通块都满足$\sum d_{x,y,z} \equiv 0 \pmod 2$的$a,b,c$的数量，就能够快速统计贡献。

我们考虑某一组循环节（那个$la\times lb\times lc$的正方体）的某一个连通块对$a,b,c$的限制，设循环节包含的每个维度的下标集合为$a’,b’,c’$，则限制为

$$\sum_{x\in a'} a_x \operatorname{lcm}{\{la,lb,lc\}\over la} +\sum_{x\in b'} b_x \operatorname{lcm}{\{la,lb,lc\}\over lb} + \sum_{x\in c'} c_x {\operatorname{lcm}\{la,lb,lc\}\over lc} \equiv 0 \pmod 2$$

现在将每一个$a_x,b_x,c_x$看做未知数，则问题转化成求方程的解数，是一个经典的线性基问题。

由于数据范围很小，可以直接打表。

下面是我的代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <bitset>
#define PB push_back
#define MP make_pair
#define PII pair<int,int>
#define FIR first
#define SEC second
#define ll long long
using namespace std;
template <class T>
inline void rd(T &x) {
	x=0; char c=getchar(); int f=1;
	while(!isdigit(c)) { if(c=='-') f=-1; c=getchar(); }
	while(isdigit(c)) x=x*10-'0'+c,c=getchar(); x*=f;
}
const int mod=998244353;
int Pow(int x,int y) {
    int res=1;
    for(;y;x=x*(ll)x%mod,y>>=1)
        if(y&1) res=res*(ll)x%mod;
    return res;
}
int lcm[20][20][20];
int fac[20],inv[20],ipw[8000],pw[8000];
int Inv[20];
vector<vector<PII> > g[20];
namespace Mat {
    bitset<39> f[39],b;
    int m,cnt;
    void init(int len) { for(int i=0;i<m;++i) f[i].reset(); m=len,cnt=0; }
    void ins(int l,int r,int x) {
        if(x&1) for(int i=l;i<r;++i) b[i]=1;
    }
    void Ins() {
        // cout<<"INS:"; for(int i=0;i<m;++i) cout<<(b[i]==1); cout<<endl;
        for(int i=0;i<m;++i) if(b[i]) {
            if(f[i][i]) b^=f[i];
            else {
                f[i]=b,cnt++;
                break;
            }
        }
        b.reset();
    }
    int sol() { return cnt; }
    void Debug() {
        for(int i=0;i<m;++i,puts(""))
            for(int j=0;j<m;++j) cout<<(f[i][j]==1);
    }
}
namespace predo_calc {
    int gcd(int a,int b) { return b?gcd(b,a%b):a; }
    int LCM(int a,int b) { return a/gcd(a,b)*b; }
    vector<PII> s;
    int cur;
    void dfs(int u,int tot) {
        if(tot==cur) { g[cur].PB(s); return; }
        if(tot+u>cur) return;
        dfs(u+1,tot);
        for(int j=1;tot+j*u<=cur;++j) {
            s.PB(MP(u,j));
            dfs(u+1,tot+j*u);
            s.pop_back();
        }
    }
    void getpw(int n) {
        pw[0]=1; for(int i=1;i<=n;++i) pw[i]=pw[i-1]*2ll%mod;
        ipw[n]=Pow(pw[n],mod-2); for(int i=n;i>=1;--i) ipw[i-1]=ipw[i]*2ll%mod;
    }
    void predo(int n) {
        for(int i=1;i<=n;++i) Inv[i]=Pow(i,mod-2);
        fac[0]=1; for(int i=1;i<=n;++i) fac[i]=fac[i-1]*(ll)i%mod;
        inv[n]=Pow(fac[n],mod-2); for(int i=n;i>=1;--i) inv[i-1]=inv[i]*(ll)i%mod;
        getpw(n*n*n);
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j)
                for(int k=1;k<=n;++k)
                    lcm[i][j][k]=LCM(LCM(i,j),k);
        for(int i=1;i<=n;++i) cur=i,dfs(1,0);
    }
}
int sol(int A,int B,int C) {
    int ans=0;
    for(int pa=0;pa<g[A].size();++pa)
    for(int pb=0;pb<g[B].size();++pb)
    for(int pc=0;pc<g[C].size();++pc) {
        int tans=1;
        vector<PII> &pA=g[A][pa],&pB=g[B][pb],&pC=g[C][pc];
        for(int j=0;j<pA.size();++j) tans=tans*(ll)inv[pA[j].SEC]%mod*Pow(Inv[pA[j].FIR],pA[j].SEC)%mod;
        for(int j=0;j<pB.size();++j) tans=tans*(ll)inv[pB[j].SEC]%mod*Pow(Inv[pB[j].FIR],pB[j].SEC)%mod;
        for(int j=0;j<pC.size();++j) tans=tans*(ll)inv[pC[j].SEC]%mod*Pow(Inv[pC[j].FIR],pC[j].SEC)%mod;
        Mat::init(A+B+C);
        for(int iA=0,tA=0;iA<pA.size();++iA)
        for(int jA=0;jA<pA[iA].SEC;++jA,tA+=pA[iA].FIR)
            for(int iB=0,tB=A;iB<pB.size();++iB)
            for(int jB=0;jB<pB[iB].SEC;++jB,tB+=pB[iB].FIR)
                for(int iC=0,tC=A+B;iC<pC.size();++iC)
                for(int jC=0;jC<pC[iC].SEC;++jC,tC+=pC[iC].FIR) {
                    int a=pA[iA].FIR,b=pB[iB].FIR,c=pC[iC].FIR;
                    tans=tans*(ll)pw[a*b*c/lcm[a][b][c]]%mod;
                    Mat::ins(tA,tA+pA[iA].FIR,lcm[a][b][c]/a);
                    Mat::ins(tB,tB+pB[iB].FIR,lcm[a][b][c]/b);
                    Mat::ins(tC,tC+pC[iC].FIR,lcm[a][b][c]/c);
                    Mat::Ins();
                }
        tans=tans*(ll)pw[A+B+C-Mat::sol()]%mod;
        // Mat::Debug();
        ans=(ans+tans)%mod;
    }
    ans=ans*(ll)ipw[A+B+C]%mod;
}

int main() {
    predo_calc::predo(13);
    int T; rd(T);
    while(T--) {
        int A,B,C; rd(A),rd(B),rd(C);
        cout<<sol(A,B,C)<<endl;
    }
    return 0;
}